练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．如果关于x的方程（m+2）x=8无解，那么m的取值范围是（　　）
    A．m=-2B．m＞-2C．m≠-2D．任意实数

    分析 根据等式不相等，可得答案．

    解答 解：由题意，得
    m+2=0，
    解得m=-2，
    故选：A．

    点评 本题考查了解一元一次方程，根据题意得出关于m的方程是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    10．如图，在Rt△ABC中，∠ACB=90°，AC=8，AB=10，DE是△ABC的中位线，则
    DE=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

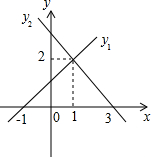    11．已知函数y1=k1x+b1与函数y2=k2x+b2的图象如图所示，则不等式y1＞y2的解集是（　　）
    A．x＜1B．x＞1C．x＜2D．x＞3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．解不等式组$\left\{\begin{array}{l}3x＞2x-1\\ x≤3（2-x）\end{array}\right.$，并求出它的非负整数解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

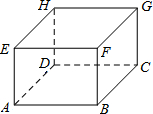    15．如图，在长方体ABCD-EFGH中，可以把平面ABFE与平面BCGF组成的图形看作直立于面ABCD上的合页形折纸，从而说明棱BF垂直于平面ABCD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知：如图，正方形ABCD的边长为2，动点E从点A出发，沿着A-B-C的方向以每秒钟1个单位长度的速度匀速运动，当点E到达点C时运动停止．联结DE，以DE为边作正方形DEFG．设运动的时间为x秒．
    （1）如图①，当点E在边AB上时，联结CG，求证：AE=CG；
    （2）如图②，当点E在边BC上时，设正方形ABCD与正方形DEFG重叠部分的面积为y，求y关于x的函数解析式，并写出自变量x的取值范围；
    （3）直接写出，在点E的运动过程中，对应的点F的运动路径的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

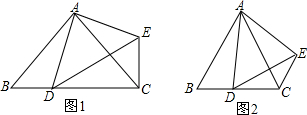    12．在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．
    （1）如图1，当点D在直线BC上，如果∠BAC=90°，
    求证：CE+DC=BC
    证明：∵∠BAC=∠DAE（已知）
    ∴∠BAC-∠DAC=∠DAE-∠DAC
    即∠BAD=∠CAE
    在△ABD与△ACE中，
    $\left\{\begin{array}{l}{AB=AC（已知）}\\{∠BAD=∠CAE（已求）}\\{AD=AE（已知）}\end{array}\right.$
    ∴△ABD≌△ACE（SAS）
    ∴BD=CE（全等三角形的对应法相等）
    ∵BD+DC=BC
    ∴CE+DC=BC．
    （2）如图1，在（1）条件下，求：∠BCE的度数？
    （3）如图2，当点D在线段BC上移动，设∠BAC=α，∠BCE=β，则α，β之间有怎样的数量关系？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

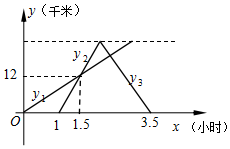    9．甲乙两人先后由A地沿同一路线前往B地，甲先出发，一小时后乙再出发，半小时后在离A地12千米处乙追上甲，此时两人正好到达AB的中点．然后两人各自保持原速不变，先后到达B地．若甲由A地出发的行驶时间为x小时，甲、乙离开A地的距离为y1千米和y2千米，函数图象如图所示．
    （1）请直接写出甲的速度是80千米/小时；
    （2）求y2关于x的函数关系式（不写x的取值范围）；
    （3）乙到达B地后立即从原路返回A地．过程中，他离开A地的距离y3（千米）关于x（小时）的函数图象如图所示．请直接写出乙在返回途中与甲相遇时，x=2.5小时．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．0.000043米用科学记数法表示，正确的是（　　）
    A．4.3×10-4B．4.3×10-5C．4.3×10-6D．43×10-5

    查看答案和解析>>

    同步练习册答案