
ЁОЬтФПЁПвбжЊШчЭМЃЌЁЯCOD=90ЁуЃЌжБЯпABгыOCНЛгкЕуBЃЌгыODНЛгкЕуAЃЌЩфЯпOEКЭЩфЯпAFНЛгкЕуGЃЎ
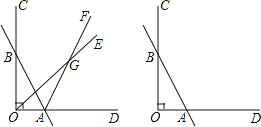
ЃЈ1ЃЉШєOEЦНЗжЁЯBOAЃЌAFЦНЗжЁЯBADЃЌЁЯOBA=30ЁуЃЌдђЁЯOGA= .
ЃЈ2ЃЉШєЁЯGOA=![]() ЁЯBOAЃЌЁЯGAD=
ЁЯBOAЃЌЁЯGAD=![]() ЁЯBADЃЌЁЯOBA=30ЁуЃЌдђЁЯOGA= .
ЁЯBADЃЌЁЯOBA=30ЁуЃЌдђЁЯOGA= .
ЃЈ3ЃЉНЋЃЈ2ЃЉжаЁАЁЯOBA=30ЁуЁБИФЮЊЁАЁЯOBA=ІСЁБЃЌЦфгрЬѕМўВЛБфЃЌдђЁЯOGA= ЃЈгУКЌІСЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ4ЃЉШєOEНЋЁЯBOAЗжГЩ1ЃК2СНВПЗжЃЌAFЦНЗжЁЯBADЃЌЁЯABO=ІСЃЈ30ЁуЃМІСЃМ90ЁуЃЉЃЌЧѓЁЯOGAЕФЖШЪ§ЃЈгУКЌІСЕФДњЪ§ЪНБэЪОЃЉ
ЁОД№АИЁПЃЈ1ЃЉ15ЁуЃЛЃЈ2ЃЉ10ЁуЃЛЃЈ3ЃЉ![]() ІСЃЛЃЈ4ЃЉ
ІСЃЛЃЈ4ЃЉ![]() ІС+15ЁуЛђ
ІС+15ЁуЛђ![]() ІС-15ЁуЃЎ
ІС-15ЁуЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉгЩгкЁЯBAD=ЁЯABO+ЁЯBOA=ІС+90ЁуЃЌгЩAFЦНЗжЁЯBADЕУЕНЁЯFAD=![]() ЁЯBADЃЌЖјЁЯFAD=ЁЯEOD+ЁЯOGAЃЌ2ЁС45Ёу+2ЁЯOGA=ІС+90ЁуЃЌдђЁЯOGA=
ЁЯBADЃЌЖјЁЯFAD=ЁЯEOD+ЁЯOGAЃЌ2ЁС45Ёу+2ЁЯOGA=ІС+90ЁуЃЌдђЁЯOGA=![]() ІСЃЌШЛКѓАбІС=30ЁуДњШыМЦЫуМДПЩЃЛ
ІСЃЌШЛКѓАбІС=30ЁуДњШыМЦЫуМДПЩЃЛ
ЃЈ2ЃЉгЩгкЁЯGOA=![]() ЁЯBOA=30ЁуЃЌЁЯGAD=
ЁЯBOA=30ЁуЃЌЁЯGAD=![]() ЁЯBADЃЌЁЯOBA=ІСЃЌИљОнЁЯFAD=ЁЯEOD+ЁЯOGAЕУЕН3ЁС30Ёу+3ЁЯOGA=ІС+90ЁуЃЌдђЁЯOGA=
ЁЯBADЃЌЁЯOBA=ІСЃЌИљОнЁЯFAD=ЁЯEOD+ЁЯOGAЕУЕН3ЁС30Ёу+3ЁЯOGA=ІС+90ЁуЃЌдђЁЯOGA=![]() ІСЃЌШЛКѓАбІС=30ЁуДњШыМЦЫуЃЛ
ІСЃЌШЛКѓАбІС=30ЁуДњШыМЦЫуЃЛ
ЃЈ3ЃЉгЩЃЈ2ЃЉЕУЕНЁЯOGA=![]() ІСЃЛ
ІСЃЛ
ЃЈ4ЃЉЬжТлЃКЕБЁЯEODЃКЁЯCOE=1ЃК2ЪБЃЌРћгУЁЯBAD=ЁЯABO+ЁЯBOA=ІС+90ЁуЃЌЁЯFAD=ЁЯEOD+ЁЯOGAЕУЕН2ЁС30Ёу+2ЁЯOGA=ІС+90ЁуЃЌдђЁЯOGA=![]() ІС+15ЁуЃЛ
ІС+15ЁуЃЛ
ЕБЁЯEODЃКЁЯCOE=2ЃК1ЪБЃЌдђЁЯEOD=60ЁуЃЌЭЌРэЕУЁЯOGA=![]() ІС-15ЁуЃЎ
ІС-15ЁуЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉ15ЁуЃЛ

ЃЈ2ЃЉ10ЁуЃЛ
ЃЈ3ЃЉ![]() ІСЃЛ
ІСЃЛ
ЃЈ4ЃЉЕБЁЯEODЃКЁЯCOE=1ЃК2ЪБЃЌ
дђЁЯEOD=30ЁуЃЌ
ЁпЁЯBAD=ЁЯABO+ЁЯBOA=ІС+90ЁуЃЌ
ЖјAFЦНЗжЁЯBADЃЌ
ЁрЁЯFAD=![]() ЁЯBADЃЌ
ЁЯBADЃЌ
ЁпЁЯFAD=ЁЯEOD+ЁЯOGAЃЌ
Ёр2ЁС30Ёу+2ЁЯOGA=ІС+90ЁуЃЌ
ЁрЁЯOGA=![]() ІС+15ЁуЃЛ
ІС+15ЁуЃЛ
ЕБЁЯEODЃКЁЯCOE=2ЃК1ЪБЃЌдђЁЯEOD=60ЁуЃЌ
ЭЌРэЕУЕНЁЯOGA=![]() ІС-15ЁуЃЌ
ІС-15ЁуЃЌ
МДЁЯOGAЕФЖШЪ§ЮЊ![]() ІС+15ЁуЛђ
ІС+15ЁуЛђ![]() ІС-15ЁуЃЎ
ІС-15ЁуЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЪаФГжабЇЦпЁЂАЫФъМЖИїбЁХЩ10УћбЁЪжВЮМгбЇаЃОйАьЕФЁААЎЮвОЃУХЁБжЊЪЖОКШќЃЌМЦЗжВЩгУ10ЗжжЦЃЌбЁЪжЕУЗжОљЮЊећЪ§ЃЌГЩМЈДяЕН6ЗжЛђ6ЗжвдЩЯЮЊКЯИёЃЌДяЕН9ЗжЛђ10ЗжЮЊгХауЃЎетДЮОКШќКѓЃЌЦпЁЂАЫФъМЖСНжЇДњБэЖгбЁЪжГЩМЈЗжВМЕФЬѕаЮЭГМЦЭМКЭГЩМЈЭГМЦЗжЮіБэШчЯТЃЌЦфжаЦпФъМЖДњБэЖгЕУ6ЗжЁЂ10ЗжЕФбЁЪжШЫЪ§ЗжБ№ЮЊaЃЌbЃЎ
ЖгБ№ | ЦНОљЗж | жаЮЛЪ§ | ЗНВю | КЯИёТЪ | гХауТЪ |
ЦпФъМЖ | 6.7 | m | 3.41 | 90% | n |
АЫФъМЖ | 7.1 | 7.5 | 1.69 | 80% | 10% |
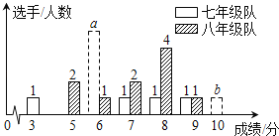
ЃЈ1ЃЉЧывРОнЭМБэжаЕФЪ§ОнЃЌЧѓaЃЌbЕФжЕЃЛ
ЃЈ2ЃЉжБНгаДГіБэжаЕФmЃЌnЕФжЕЃЛ
ЃЈ3ЃЉгаШЫЫЕЦпФъМЖЕФКЯИёТЪЁЂгХауТЪОљИпгкАЫФъМЖЃЌЫљвдЦпФъМЖЖгГЩМЈБШАЫФъМЖЖгКУЃЌЕЋвВгаШЫЫЕАЫФъМЖЖгГЩМЈБШЦпФъМЖЖгКУЃЎЧыФуИјГіСНЬѕжЇГжАЫФъМЖЖгГЩМЈКУЕФРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌAB=4ЃЌЁЯBADЕФЦНЗжЯпгыBCЕФбгГЄЯпНЛгкЕуEЃЌгыDCНЛгкЕуFЃЌЧвЕуFЮЊБпDCЕФжаЕуЃЌDGЁЭAEЃЌДЙзуЮЊGЃЌШєDG=1ЃЌдђAEЕФБпГЄЮЊЃЈ ЃЉ

AЃЎ2![]() BЃЎ4
BЃЎ4![]() CЃЎ4 DЃЎ8
CЃЎ4 DЃЎ8
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтжаЃЌе§ШЗЕФгаЃЈ ЃЉ
ЂйRtЁїABCжаЃЌвбжЊСНБпГЄЗжБ№ЮЊ3КЭ4ЃЌдђЕкШ§БпГЄЮЊ5ЃЛ
ЂкгавЛИіФкНЧЕШгкЦфЫћСНИіФкНЧКЭЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃЛ
ЂлШ§НЧаЮЕФШ§БпЗжБ№ЮЊaЃЌbЃЌCЃЌШєa2+c2=b2ЃЌФЧУДЁЯC=90ЁуЃЛ
ЂмШєЁїABCжаЃЌЁЯAЃКЁЯBЃКЁЯC=1ЃК5ЃК6ЃЌдђЁїABCЪЧжБНЧШ§НЧаЮЃЎ
AЃЎ1Иі BЃЎ2Иі CЃЎ3Иі DЃЎ4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвдЯТИїзщЯпЖЮЮЊБпВЛФмзщГЩШ§НЧаЮЕФЪЧЃЈЁЁЁЁЃЉ
A. 1ЃЌ5ЃЌ6 B. 4ЃЌ3ЃЌ3 C. 2ЃЌ5ЃЌ4 D. 5ЃЌ8ЃЌ4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгавЛзщЪ§ОнЃК1ЃЌ3ЃЌ3ЃЌ4ЃЌ5ЃЌетзщЪ§ОнЕФжкЪ§ЮЊЃЈ ЃЉ
AЃЎ1 BЃЎ3 CЃЎ4 DЃЎ5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНЭЌбЇгУвЛИБЦЫПЫХЦжаХЦУцЪ§зжЗжБ№ЪЧЃК3ЃЌ4ЃЌ5ЃЌ6ЕФ4еХХЦзіГщЪ§бЇгЮЯЗЃЎгЮЯЗЙцдђЪЧЃКНЋет4еХХЦЕФе§УцШЋВПГЏЯТЃЌЯДдШЃЌДгжаЫцЛњГщШЁвЛеХЃЌГщЕУЕФЪ§зїЮЊЪЎЮЛЩЯЕФЪ§зжЃЌШЛКѓЃЌНЋЫљГщЕФХЦЗХЛиЃЌе§УцШЋВПГЏЯТЁЂЯДдШЃЌдйДгжаЫцЛњГщШЁвЛеХЃЌГщЕУЕФЪ§зїЮЊИіЮЛЩЯЕФЪ§зжЃЌетбљОЭЕУЕНвЛИіСНЮЛЪ§ЃЎШєетИіСНЮЛЪ§аЁгк45ЃЌдђМзЛёЪЄЃЌЗёдђввЛёЪЄЃЎФуШЯЮЊетИігЮЯЗЙЋЦНТ№ЃПЧыдЫгУИХТЪжЊЪЖЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЯТСаНсТлЃКЂйдкЪ§жсЩЯЕФЕужЛФмБэЪОЮоРэЪ§ЃЛЂкШЮКЮвЛИіЮоРэЪ§ЖМФмгУЪ§жсЩЯЕФЕуБэЪОЃЛЂлЪЕЪ§гыЪ§жсЩЯЕФЕувЛвЛЖдгІЃЛЂмгаРэЪ§гаЮоЯоИіЃЌЮоРэЪ§гаЯоИіЃЌЦфжае§ШЗЕФНсТлЪЧЃЈ ЃЉ
A.ЂйЂк
B.ЂкЂл
C.ЂлЂм
D.ЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=![]() x2+bxЉ2гыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкCЕуЃЌЧвAЃЈвЛ1ЃЌ0ЃЉЃЎ
x2+bxЉ2гыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкCЕуЃЌЧвAЃЈвЛ1ЃЌ0ЃЉЃЎ
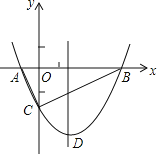
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНМАЖЅЕуDЕФзјБъЃЛ
ЃЈ2ЃЉХаЖЯЁїABCЕФаЮзДЃЌжЄУїФуЕФНсТлЃЛ
ЃЈ3ЃЉЕуMЪЧХзЮяЯпЖдГЦжсЩЯЕФвЛИіЖЏЕуЃЌЕБЁїACMжмГЄзюаЁЪБЃЌЧѓЕуMЕФзјБъМАЁїACMЕФзюаЁжмГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com