
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
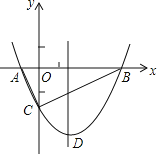
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
【答案】(1)抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣2.顶点D的坐标为:(
x﹣2.顶点D的坐标为:(![]() ,﹣
,﹣![]() );(2)△ABC是直角三角形.(3)3
);(2)△ABC是直角三角形.(3)3![]() .
.
【解析】
试题分析:(1)直接将(﹣1,0),代入解析式进而得出答案,再利用配方法求出函数顶点坐标;
(2)分别得出AB2=25,AC2=OA2+OC2=5,BC2=OC2+OB2=20,进而利用勾股定理的逆定理得出即可;
(3)利用轴对称最短路线求法得出M点位置,再求△ACM周长最小值.
解:(1)∵点A(﹣1,0)在抛物线y=![]() x2+bx﹣2上,
x2+bx﹣2上,
∴![]() ×(﹣1 )2+b×(﹣1)﹣2=0,
×(﹣1 )2+b×(﹣1)﹣2=0,
解得:b=﹣![]() ,
,
∴抛物线的解析式为y=![]() x2﹣
x2﹣![]() x﹣2.
x﹣2.
y=![]() (x﹣
(x﹣![]() )2﹣
)2﹣![]() ,
,
∴顶点D的坐标为:(![]() ,﹣
,﹣![]() );
);
(2)当x=0时y=﹣2,∴C(0,﹣2),OC=2.
当y=0时,![]() x2﹣
x2﹣![]() x﹣2=0,
x﹣2=0,
解得:x1=﹣1,x2=4,
∴B (4,0),
∴OA=1,OB=4,AB=5.
∵AB2=25,AC2=OA2+OC2=5,BC2=OC2+OB2=20,
∴AC2+BC2=AB2.
∴△ABC是直角三角形.
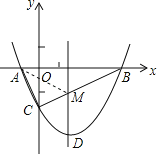
(3)如图所示:连接AM,
点A关于对称轴的对称点B,BC交对称轴于点M,根据轴对称性及两点之间线段最短可知,
MC+MA的值最小,即△ACM周长最小,
设直线BC解析式为:y=kx+d,则![]() ,
,
解得: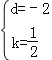 ,
,
故直线BC的解析式为:y=![]() x﹣2,
x﹣2,
当x=![]() 时,y=﹣
时,y=﹣![]() ,
,
∴M(![]() ,﹣
,﹣![]() ),
),
△ACM最小周长是:AC+AM+MC=AC+BC=![]() +2
+2![]() =3
=3![]() .
.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知如图,∠COD=90°,直线AB与OC交于点B,与OD交于点A,射线OE和射线AF交于点G.
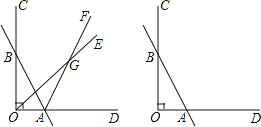
(1)若OE平分∠BOA,AF平分∠BAD,∠OBA=30°,则∠OGA= .
(2)若∠GOA=![]() ∠BOA,∠GAD=
∠BOA,∠GAD=![]() ∠BAD,∠OBA=30°,则∠OGA= .
∠BAD,∠OBA=30°,则∠OGA= .
(3)将(2)中“∠OBA=30°”改为“∠OBA=α”,其余条件不变,则∠OGA= (用含α的代数式表示)
(4)若OE将∠BOA分成1:2两部分,AF平分∠BAD,∠ABO=α(30°<α<90°),求∠OGA的度数(用含α的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去冬今春,某市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某镇中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)、求饮用水和蔬菜各有多少件?
(2)、现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该镇中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)、在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A(x1,y1)和B(x2,y2)都在直线y=3x+2上,且x1>x2,则y1与y2的关系是( )
A. y1≤y2 B. y1≥y2 C. y1<y2 D. y1>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,把一张长方形的纸片ABCD沿对角线BD折叠,点C落在E处,BE交AD于点F.
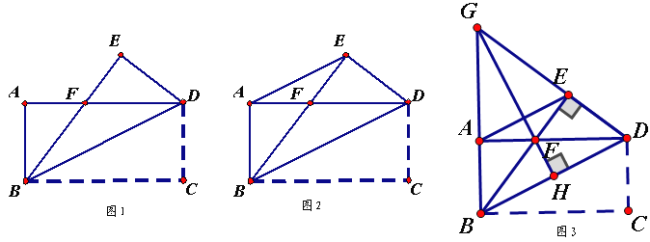
(1)求证:FB=FD;
(2)如图2,连接AE,求证:AE∥BD;
(3)如图3,延长BA,DE相交于点G,连接GF并延长交BD于点H,求证:GH垂直平分BD。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的个数是( ).
(1)两个无理数的和必是无理数;
(2)两个无理数的积必是无理数;
(3)无理数包括正无理数,0,负无理数;
(4)实数与数轴上的点是一一对应的.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com