
【题目】如图1,把一张长方形的纸片ABCD沿对角线BD折叠,点C落在E处,BE交AD于点F.
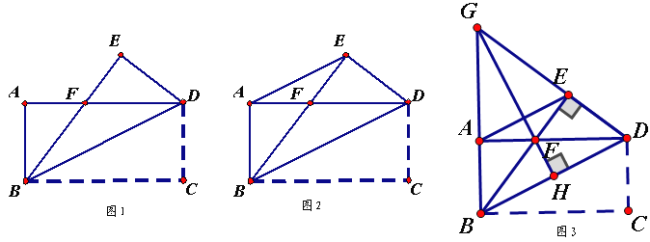
(1)求证:FB=FD;
(2)如图2,连接AE,求证:AE∥BD;
(3)如图3,延长BA,DE相交于点G,连接GF并延长交BD于点H,求证:GH垂直平分BD。
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
试题分析:(1)根据矩形的性质和折叠的性质可得:AB=DC=DE,∠BAD=∠BCD=∠BED=90°,根据AAS可证△ABF≌△EDF,根据全等三角形的性质可证BF=DF;
(2)根据全等三角形的性质可证:FA=FE,根据等边对等角可得:∠FAE=∠FEA,根据三角形内角和定理可证:2∠AEF +∠AFE =2∠FBD+∠BFD =180°,所以可证∠AEF=∠FBD,根据内错角相等,两直线平行可证AE∥BD;
(3)根据矩形的性质可证:AD=BC=BE,AB=CD=DE,BD=DB,根据SSS可证:△ABD≌△EDB,根据全等三角形的性质可证:∠ABD=∠EDB,根据等角对等边可证:GB=GD,根据HL可证:△AFG≌△EFG,根据全等三角形的性质可证:∠AGF=∠EGF,所以GH垂直平分BD.
试题解析:(1)∵长方形ABCD,
∴AB=DC=DE,∠BAD=∠BCD=∠BED=90°,
在△ABF和△DEF中,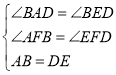
∴△ABF≌△EDF(AAS),
∴BF=DF.
(2)∵△ABF≌△EDF,
∴FA=FE,
∴∠FAE=∠FEA,
又∵∠AFE=∠BFD,且2∠AEF +∠AFE =2∠FBD+∠BFD =180°,
∴∠AEF=∠FBD,
∴AE∥BD,
(3)∵长方形ABCD,
∴AD=BC=BE,AB=CD=DE,BD=DB,
∴△ABD≌△EDB(SSS),
∴∠ABD=∠EDB,
∴GB=GD,
在△AFG和△EFG中,
∠GAF=∠GEF=90°,
FA=FE,
FG=FG,
∴△AFG≌△EFG(HL),
∴∠AGF=∠EGF,
∴GH垂直平分BD.
【方法II】
(1)∵△BCD≌△BED,
∴∠DBC=∠EBD
又∵长方形ABCD,
∴AD∥BC,
∴∠ADB=∠DBC,
∴∠EBD=∠ADB,
∴FB=FD.
(2)∵长方形ABCD,
∴AD=BC=BE,
又∵FB=FD,
∴FA=FE,
∴∠FAE=∠FEA,
又∵∠AFE=∠BFD,且2∠AEF +∠AFE =2∠FBD+∠BFD =180°,
∴∠AEF=∠FBD,
∴AE∥BD,
(3)∵长方形ABCD,
∴AD=BC=BE,AB=CD=DE,BD=DB,
∴△ABD≌△EDB,
∴∠ABD=∠EDB,
∴GB=GD,
又∵FB=FD,
∴GF是BD的垂直平分线,
即GH垂直平分BD.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知下列结论:①在数轴上的点只能表示无理数;②任何一个无理数都能用数轴上的点表示;③实数与数轴上的点一一对应;④有理数有无限个,无理数有限个,其中正确的结论是( )
A.①②
B.②③
C.③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
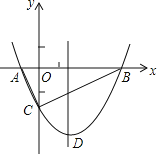
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM周长最小时,求点M的坐标及△ACM的最小周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】试用学过的知识判断,下列说法正确的是( )
A. 一个直角三角形一定不是等腰三角形 B. 一个等腰三角形一定不是锐角三角形
C. 一个等腰三角形一定不是等腰三角形 D. 一个等腰三角形一定不是钝角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如下图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)△ABC的面积为 ;
(2)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B',补全△A′B′C′;
(3)在图中画出△ABC的高CD;
(4)若连接![]() ,
, ![]() ,则这两条线段之间的关系是 ;
,则这两条线段之间的关系是 ;
(5)能使S△ABC=S△QBC的格点Q,共有 个.
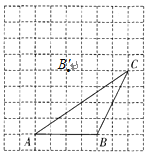
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “任意画一个三角形,其内角和为360°”是随机事件;
B. 已知某篮球运动员投篮投中的概率为0.6,则他投十次可投中6次;
C. 抽样调查选取样本时,所选样本可按自己的喜好选取;
D. 检测某城市的空气质量,采用抽样调查法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com