
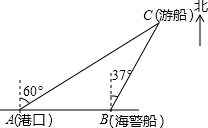
 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以每小时40海里的速度前往救援,则海警船到达事故船C处所需的时间大约为(单位:小时)( )
一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以每小时40海里的速度前往救援,则海警船到达事故船C处所需的时间大约为(单位:小时)( )| A. | $\frac{1}{sin37°}$ | B. | $\frac{1}{cos37°}$ | C. | sin37° | D. | cos37° |
分析 过点C作CD⊥AB交AB延长线于D.先解Rt△ACD得出CD=$\frac{1}{2}$AC=40海里,再解Rt△CBD中,得出BC=$\frac{CD}{cos∠BCD}$=$\frac{40}{cos37°}$海里,然后根据时间=路程÷速度即可求出海警船到大事故船C处所需的时间.
解答 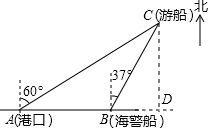 解:如图,过点C作CD⊥AB交AB延长线于D.
解:如图,过点C作CD⊥AB交AB延长线于D.
在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80海里,
∴CD=$\frac{1}{2}$AC=40海里.
在Rt△CBD中,∵∠CDB=90°,∠BCD=37°,
∴BC=$\frac{CD}{cos∠BCD}$=$\frac{40}{cos37°}$海里,
∴海警船到大事故船C处所需的时间大约为:$\frac{40}{cos37°}$÷40=$\frac{1}{cos37°}$(小时).
故选B.
点评 本题考查了解直角三角形的应用-方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:选择题
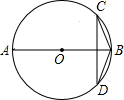 如图,已知AB是⊙O的直径,弦CD⊥AB,连结BD、BC,若∠ABD=56°,则∠C的度数为( )
如图,已知AB是⊙O的直径,弦CD⊥AB,连结BD、BC,若∠ABD=56°,则∠C的度数为( )| A. | 28° | B. | 34° | C. | 44° | D. | 56° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)计算:$\sqrt{8}$-(π-1)0-4sin45°;
(1)计算:$\sqrt{8}$-(π-1)0-4sin45°;查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 工种 属地 | 钳工 | 车工 |
| A地 | 1800(元/月) | 1600(元/月) |
| B地 | 1600(元/月) | 1200(元/月) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k1+k2<0 | B. | k1+k2>0 | C. | k1k2<0 | D. | k1k2>0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<d<e<n | B. | d<m<n<e | C. | d<m<e<n | D. | m<d<n<e |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
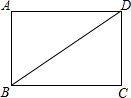 如图,BD是矩形ABCD的一条对角线.
如图,BD是矩形ABCD的一条对角线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com