
【题目】如图,小圆圈表示网络的结点,结点之间的连线表示它们之间有网线相联,连线标注的数字表示该网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,由单位时间内传递的最大信息量为( ).

A.19B.20C.24D.26
【答案】A
【解析】
要想求得单位时间内从结点A向结点B传递的最大信息量,关键是分析出每段网线在单位时间内传递的最大信息量.
解:依题意,首先找出A到B的路线,
①单位时间内从结点A经过上面一个中间节点向结点B传递的最大信息量,从结点A向中间的结点传出12个信息量,在该结点处分流为6个和5个,此时信息量为11;再传到结点B最大传递分别是4个和3个,此时信息量为3+4=7个.
②单位时间内从结点A经过下面一个中间结点向结点B传递的最大信息量是12个信息量,在中间结点分流为6个和8个,但此时总信息量为12(因为总共只有12个信息量);再往下到结点B最大传递7个但此时前一结点最多只有6个,另一条路线到最大只能传输6个结点B,所以此时信息量为6+6=12个.
③综合以上结果,单位时间内从结点A向结点B传递的最大信息量是3+4+6+6=7+12=19个.
故选:A.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,D为∠BAC的外角平分线上一点,并且满足BD=CD,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①![]() ;②∠DBC=∠DCB;③CE=AB+AE④∠BDC=∠BAC,其中正确的结论有( )
;②∠DBC=∠DCB;③CE=AB+AE④∠BDC=∠BAC,其中正确的结论有( )
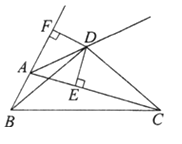
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区计划对该社区的区域进行绿化,经投标,由甲、乙两个施工队来完成,已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,若两队独立完成面积为![]() 区域的绿化时,甲队比乙队少用3天,求甲、乙两施工队每天分别能完成绿化的面积是多少?
区域的绿化时,甲队比乙队少用3天,求甲、乙两施工队每天分别能完成绿化的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,下列条件中,不能说明AB⊥CD的是( )

A. ∠AOD=90°
B. ∠AOC=∠BOC
C. ∠BOC+∠BOD=180°
D. ∠AOC+∠BOD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形网格纸中,格线与格线的交点称为格点,以格点为顶点的三角形称为格点三角形,△ABC就是一个格点三角形.
(1)请画出△ABC关于直线l对称的格点△A1B1C1;
(2)将线段AC向左平移3个单位长度,再向下平移5个单位长度,画出平移后得到的线段A2C2,并以它为一边作格点△A2B2C2,使得A2B2=C2B2,满足条件的格点B2共有_____个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一枚棋子放在边长为1个单位长度的正六边形

ABCDEF的顶点A处,通过摸球来确定该棋子的走法,其规则是:在
一只不透明的袋子中,装有3个标号分别为1、2、3的相同小球,搅匀
后从中任意摸出1个,记下标号后放回袋中并搅匀,再从中任意摸出1
个,摸出的两个小球标号之和是几棋子就沿边按顺时针方向走几个单位
长度.
棋子走到哪一点的可能性最大?求出棋子走到该点的概率.(用列表或画树状图的方法
求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB⊥BD,AB∥ED,AB=ED,要说明△ABC≌△EDC,若以“SAS”为依据,还要添加的条件为 ;若添加条件AC=EC,则可以用 公理(或定理)判定全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B分别是直线a和b上的点,∠1=∠2,C、D在两条直线之间,且∠C=∠D.
(1) 证明:a∥b;
(2) 如图,∠EFG=60°,EF交a于H,FG交b于I,HK∥FG,若∠4=2∠3,判断∠5、∠6的数量关系,并说明理由;
(3) 如图∠EFG是平角的n分之1(n为大于1的整数),FE交a于H,FG交b于I.点J在FG上,连HJ.若∠8=n∠7,则∠9:∠10=______ .
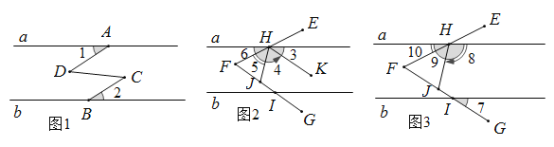
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系xOy中,把从点P出发沿纵或横方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若P(﹣1,1),Q(2,3),则P,Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.环保低碳的共享单车,正式成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为A(3,1),B(5,﹣3),C(﹣1,﹣5),若点M表示单车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com