
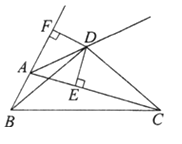
【题目】如图,D为∠BAC的外角平分线上一点,并且满足BD=CD,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①![]() ;②∠DBC=∠DCB;③CE=AB+AE④∠BDC=∠BAC,其中正确的结论有( )
;②∠DBC=∠DCB;③CE=AB+AE④∠BDC=∠BAC,其中正确的结论有( )
A.1个B.2个C.3个D.4个
【答案】D
【解析】
根据角平分线上的点到角的两边距离相等可得DE=DF,再利用“HL”证明Rt△CDE和Rt△BDF全等;根据等边对等角可证明∠DBC=∠DCB;利用“HL”证明Rt△ADE和Rt△ADF全等,根据全等三角形对应边相等可得AE=AF,CE=BF,然后易证CE=AB+AE;根据全等三角形对应角相等可得∠DBF=∠DCE,利用“8字型”可证明∠BDC=∠BAC.
解:∵AD平分∠CAF,DE⊥AC,DF⊥AB,
∴DE=DF,
在Rt△CDE和Rt△BDF中,![]() ,
,
∴Rt△CDE≌Rt△BDF(HL),故①正确;
∵BD=CD,
∴∠DBC=∠DCB,故②正确;
在Rt△ADE和Rt△ADF中,![]() ,
,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,
∵Rt△CDE≌Rt△BDF,
∴CE=BF,
∴CE=BF=AB+AF=AB+AE,故③正确;
∵Rt△CDE≌Rt△BDF,
∴∠DBF=∠DCE,
∵∠AOB=∠COD,(设AC交BD于O),
∴∠BDC=∠BAC,故④正确;
综上所述,正确的结论有①②③④共4个.
故选:D.



科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 交x轴负半轴于点A,交x轴正半轴于点B,交y轴负半轴于点C,
交x轴负半轴于点A,交x轴正半轴于点B,交y轴负半轴于点C,![]() ,
,![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 点D在抛物线
点D在抛物线![]() 在第一象限的部分上,连接BC,DC,过点D作x轴的垂线,点E为垂足,
在第一象限的部分上,连接BC,DC,过点D作x轴的垂线,点E为垂足,![]() 的正切值等于
的正切值等于![]() 的正切值的一半,求点D的坐标;
的正切值的一半,求点D的坐标;
![]() 在
在![]() 的条件下,横坐标为t的点P在抛物线
的条件下,横坐标为t的点P在抛物线![]() 在第四象限的部分上,PB的延长线交DE于点F,连接BD,OF交于点G,连接EG,若GB平分
在第四象限的部分上,PB的延长线交DE于点F,连接BD,OF交于点G,连接EG,若GB平分![]() ,求t值.
,求t值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①:MA1∥NA2,图②:MA1∥NA3,图③:MA1∥NA4,图④:MA1∥NA5,……,

则第8个图中的∠A1+∠A2+∠A3+…+∠A8=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小圆圈表示网络的结点,结点之间的连线表示它们之间有网线相联,连线标注的数字表示该网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,由单位时间内传递的最大信息量为( ).

A.19B.20C.24D.26
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com