
【题目】已知:如图∠ABC=∠ADC=90°,M,N分别是AC、BD的中点.

(1)试判断△BMD的形状,并说明理由.
(2)求证: MN⊥BD.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】陈杰骑自行车去上学,当他以往常的速度骑了一段路时,忽然想起要买某本书,于是又折回到刚经过的一家书店,买到书后继续赶去学校.以下是他本次上学的路程与所用时间的关系示意图.根据图中提供的信息回答下列问题:
(1)陈杰家到学校的距离是多少米?书店到学校的距离是多少米?
(2)陈杰在书店停留了多少分钟?本次上学途中,陈杰一共行驶了多少米?
(3)在整个上学的途中哪个时间段陈杰骑车速度最快?最快的速度是多少米?
(4)如果陈杰不买书,以往常的速度去学校,需要多少分钟?本次上学比往常多用多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,以AC为边在△ABC外作等边三角形ACD,过点D作AC的垂线,垂足为F,与AB相交于点E,连接CE.

(1)证明:AE=CE=BE;
(2)若DA⊥AB,BC=6,P是直线DE上的一点.则当P在何处时,PB+PC最小,并求出此时PB+PC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,直线MN∥GH,另一直线交GH于A,交MN于B,且∠MBA=80°,点C为直线GH上一动点,点D为直线MN上一动点,且∠GCD=50°.

(1)如图1,当点C在点A右边且点D在点B左边时,∠DBA的平分线交∠DCA的平分线于点P,求∠BPC的度数;
(2)如图2,当点C在点A右边且点D在点B右边时,∠DBA的平分线交∠DCA的平分线于点P,求∠BPC的度数;
(3)当点C在点A左边且点D在点B左边时,∠DBA的平分线交∠DCA的平分线所在直线交于点P,请直接写出∠BPC的度数,不说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
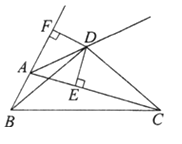
【题目】如图,D为∠BAC的外角平分线上一点,并且满足BD=CD,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①![]() ;②∠DBC=∠DCB;③CE=AB+AE④∠BDC=∠BAC,其中正确的结论有( )
;②∠DBC=∠DCB;③CE=AB+AE④∠BDC=∠BAC,其中正确的结论有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500m高度C
处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45°.求隧道AB的长
(![]() ≈1.73).
≈1.73).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,矩形ABCO的顶点![]() ,
,![]() 分别在x轴、y轴上,且
分别在x轴、y轴上,且![]() 直线
直线![]() 交y轴于点D,交x轴于点E,且
交y轴于点D,交x轴于点E,且![]() 以点E为圆心,EC为半径作
以点E为圆心,EC为半径作![]() ,交y轴负半轴于点F.
,交y轴负半轴于点F.
![]() 求直线DE的解析式;
求直线DE的解析式;
![]() 当
当![]() 与直线AB相切时,求a的值;
与直线AB相切时,求a的值;
![]() 如图2,过F作DE的垂线交
如图2,过F作DE的垂线交![]() 于点G,连结GE并延长交
于点G,连结GE并延长交![]() 于点H,连结GD,FH.
于点H,连结GD,FH.
![]() 求
求![]() 的值;
的值;
![]() 试探究
试探究![]() 的值是否与a有关?若有关,请用含a的代数式表示;若无关,则求出它的值.
的值是否与a有关?若有关,请用含a的代数式表示;若无关,则求出它的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形网格纸中,格线与格线的交点称为格点,以格点为顶点的三角形称为格点三角形,△ABC就是一个格点三角形.
(1)请画出△ABC关于直线l对称的格点△A1B1C1;
(2)将线段AC向左平移3个单位长度,再向下平移5个单位长度,画出平移后得到的线段A2C2,并以它为一边作格点△A2B2C2,使得A2B2=C2B2,满足条件的格点B2共有_____个.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com