
【题目】如图,△ABC中,∠ACB=90°,以AC为边在△ABC外作等边三角形ACD,过点D作AC的垂线,垂足为F,与AB相交于点E,连接CE.

(1)证明:AE=CE=BE;
(2)若DA⊥AB,BC=6,P是直线DE上的一点.则当P在何处时,PB+PC最小,并求出此时PB+PC的值.
【答案】(1)详见解析;(2)当点P与点E共点时,PB+PC的值最小,最小值为12.
【解析】
(1)根据等边三角形“三线合一”的性质证得DE垂直平分AC;然后由等腰三角形的判定知AE=CE,根据等边对等角、直角三角形的两个锐角互余的性质以及等量代换求得∠BCE=∠B;最后根据等角对等边证得CE=BE,所以AE=CE=BE;
(2)由(1)知,DE垂直平分AC,故PC=PA;由等量代换知PB+PC=PB+PA;根据两点之间线段最短可知,当点P、B、A在同一直线上最小,所以点P在E处时最小.
解:(1)∵△ADC是等边三角形,DF⊥AC,

∴DF垂直平分线段AC,
∴AE=EC, ∴∠ACE=∠CAE, ∵∠ACB=90°,
∴∠ACE+∠BCE=90°=∠CAE+∠B=90°,
∴∠BCE=∠B, ∴CE=EB, ∴AE=CE=BE.
(2)连接PA,PB,PC.
∵DA⊥AB, ∴∠DAB=90° ,∵∠DAC=60°,
∴∠CAB=30°, ∴∠B=60°,
∴BC=AE=EB=CE=6. ∴AB=12,
∵DE垂直平分AC, ∴PC=AP, ∴PB+PC=PB+PA,
∴当PB+PC最小时,也就是PB+PA最小,即P,B,A共线时最小,
∴当点P与点E共点时,PB+PC的值最小,最小值为12.


科目:初中数学 来源: 题型:
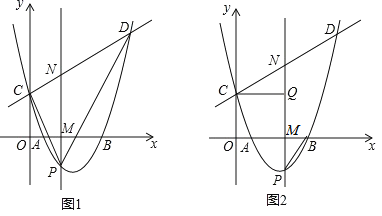
【题目】抛物线![]() 经过点
经过点![]() 和点
和点![]()
![]() 求该抛物线所对应的函数解析式;
求该抛物线所对应的函数解析式;
![]() 该抛物线与直线
该抛物线与直线![]() 相交于
相交于![]() 两点,点P是抛物线上的动点且位于x轴下方,直线
两点,点P是抛物线上的动点且位于x轴下方,直线![]() 轴,分别与x轴和直线CD交于点M、N.
轴,分别与x轴和直线CD交于点M、N.
①连结PC、PD,如图1,在点P运动过程中,![]() 的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;
的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;
②连结PB,过点C作![]() ,垂足为点Q,如图2,是否存在点P,使得
,垂足为点Q,如图2,是否存在点P,使得![]() 与
与![]() 相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.
相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校某次外出社会实践活动分为三类,因资源有限,七年级7班分配到20个名额,其中甲类2个、乙类8个、丙类10个,已知该班有50名学生,班主任准备了50个签,其中甲类、乙类、丙类按名额设置、30个空签.采取抽签的方式来确定名额分配,请解决下列问题:
(1)该班小明同学恰好抽到丙类名额的概率是多少?
(2)该班小丽同学能有幸去参加实践活动的概率是多少?
(3)后来,该班同学强烈呼吁名额太少,要求抽到甲类的概率要达到20%,则还要争取甲类名额多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丽君花卉基地出售两种盆栽花卉:太阳花6元/盆,绣球花10元/盆.若一次购买的绣球花超过20盆时,超过20盆部分的绣球花价格打8折.
(1)分别写出两种花卉的付款金额y(元)关于购买量x(盆)的函数解析式;
(2)为了美化环境,花园小区计划到该基地购买这两种花卉共90盆,其中太阳花数量不超过绣球花数量的一半.两种花卉各买多少盆时,总费用最少,最少总费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)2014年12月28日“青烟威荣”城际铁路正式开通,从烟台到北京的高铁里程比普快里程缩短了81千米,运行时间减少了9小时,已知烟台到北京的普快列车里程月1026千米,高铁平均时速是普快平均时速的2.5倍.
(1)求高铁列车的平均时速;
(2)某日王老师要去距离烟台大约630千米的某市参加14:00召开的会议,如果他买到
当日8:40从烟台到该是的高铁票,而且从该市火车站到会议地点最多需要1.5小时.试问在高铁列车准点到达的情况下他能在开会之前赶到吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com