
【题目】如图,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500m高度C
处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45°.求隧道AB的长
(![]() ≈1.73).
≈1.73).
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() 、
、![]() 的平分线交于
的平分线交于![]() ,
,![]() 是
是![]() 延长线上一点,且
延长线上一点,且![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() .其中所有正确结论的序号有( ).
.其中所有正确结论的序号有( ).

A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:点M,N把线段AB分割成AM、MN,NB,若以AM、MN、NB为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.
(1)如图①,已知M、N是线段AB的勾股分割点,AM=6,MN=8,求NB的长;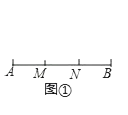
(2)如图②,在△ABC中,点D、E在边线段BC上,且BD=3,DE=5,EC=4,直线l∥BC,分别交AB、AD、AE、AC于点F、M、N、G.求证:点M,N是线段FG的勾股分割点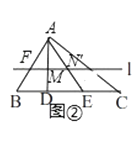
(3)在菱形ABCD中,∠ABC=β(β<90°),点E、F分别在BC、CD上,AE、AF分别交BD于点M、N.
①如图③,若BE= ![]() BC,DF=
BC,DF= ![]() CD,求证:M、N是线段BD的勾股分割点.
CD,求证:M、N是线段BD的勾股分割点.
②如图④,若∠EAF= ![]() ∠BAD,sinβ=
∠BAD,sinβ= ![]() ,当点M、N是线段AB的勾股分割点时,求BM:MN:ND的值.
,当点M、N是线段AB的勾股分割点时,求BM:MN:ND的值.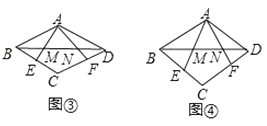
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:①abc<0;②当-1<x<3时,y>0;③a-b+c<0;④3a+c<0.其中正确的是________(填序号).
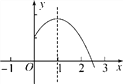
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b在数轴上的对应点如图所示,则下列式子中错误的是( )
![]()
A. a+b<0 B. a-b<0
C. -a<-b D. |a-b|=b-a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(-2,0),等边三角形AOC经过平移或轴对称或旋转对称都可以得到△OBD。
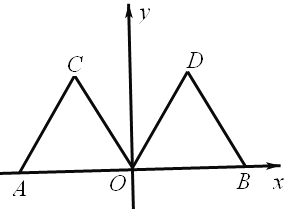
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是 个单位长度;△AOC与△OBD关于直线对称,则对称轴是 ;△AOC绕原点O顺时针旋转得到△OBD,则旋转角可以是 度;
(2)连接AD,交OC于点E,求∠AEO的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(m)与时间x(h)的函数图象为线段OA,乙队铺设完的路面长y(m)与时间x(h)的函数图象为折线BC—CD—DE,如图所示,从甲队开始工作时计时.
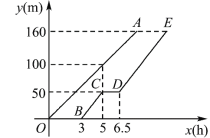
(1)求乙队铺设完的路面长y(m)与时间x(h)的函数解析式;
(2)当甲队清理完路面时,乙队还有多少米的路面没有铺设完?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com