
【题目】定义:点M,N把线段AB分割成AM、MN,NB,若以AM、MN、NB为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.
(1)如图①,已知M、N是线段AB的勾股分割点,AM=6,MN=8,求NB的长;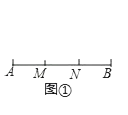
(2)如图②,在△ABC中,点D、E在边线段BC上,且BD=3,DE=5,EC=4,直线l∥BC,分别交AB、AD、AE、AC于点F、M、N、G.求证:点M,N是线段FG的勾股分割点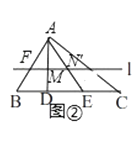
(3)在菱形ABCD中,∠ABC=β(β<90°),点E、F分别在BC、CD上,AE、AF分别交BD于点M、N.
①如图③,若BE= ![]() BC,DF=
BC,DF= ![]() CD,求证:M、N是线段BD的勾股分割点.
CD,求证:M、N是线段BD的勾股分割点.
②如图④,若∠EAF= ![]() ∠BAD,sinβ=
∠BAD,sinβ= ![]() ,当点M、N是线段AB的勾股分割点时,求BM:MN:ND的值.
,当点M、N是线段AB的勾股分割点时,求BM:MN:ND的值.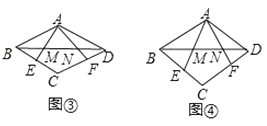
【答案】
(1)
解:当NB为最长线段时,
∵M、N是线段AB的勾股分割点,AM=6,MN=8,
∴NB= ![]() =10;
=10;
当MN为最长线段时,
NB= ![]() =2
=2 ![]() ,
,
综上所述,NB的值为10或2 ![]() ;
;
(2)
证明:如图2,∵BD=3,DE=5,EC=4,
∴DE2=BD2+EC2,
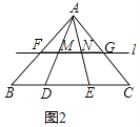
∵直线l∥BC,
∴![]() ,
,
∴可设![]() ,
,
∴FM=kBD,MN=kDE,NG=kEC,
∵DE2=BD2+EC2,
∴MN2=FM2+NG2,
∴点M,N是线段FG的勾股分割点;
(3)
解:①证明:如图3,∵四边形ABCD是菱形,
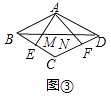
∴AD//BE,AB=BC=CD=DA,
∴△BEM∽△DAM,
∴![]() ,
,
∵BE=![]() BC,
BC,
∴BM=![]() DM,BM=
DM,BM=![]() BD,
BD,
同理可得,DN=![]() BD,
BD,
∴MN=BD﹣BM﹣DN=![]() BD,
BD,
∵MN2=![]() BD2,BM2+ND2=
BD2,BM2+ND2=![]() BD2+
BD2+![]() BD2=
BD2=![]() BD2,
BD2,
∴MN2=BM2+ND2,
∴M、N是线段BD的勾股分割点.
②如图4,将△AND绕点A顺时针旋转,旋转角等于∠BAD,则AD旋转后与AB重合,点N旋转至点K的位置,DN=BK,∠ADN=∠ABK,连接KM,
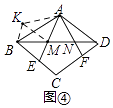
∴∠KBM=∠KBA+∠ABM=∠ABC,
∵sinβ=![]() ,
,
∴sin∠KBM=![]() ,
,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠KAM=∠NAM,
∵AN=AK,AM=AM,
∴△KAM≌△NAM,
∴KM=NM,
∵点M、N是线段BD的勾股分割点,
∴△KBM是直角三角形,
∵sin∠KBM=![]() ,
,
∴BM:MN:ND=13:12:5或BM:MN:ND=5:12:13.
【解析】(1)分两种情况进行讨论:NB为最长线段;MN为最长线段,分别根据勾股定理进行计算即可;(2)根据BD=3,DE=5,EC=4,可得DE2=BD2+EC2 , 再根据直线l∥BC,可得 ![]() =
= ![]() ,故可设
,故可设 ![]() =
= ![]() =
= ![]() =k,进而得到FM=kBD,MN=kDE,NG=kEC,再根据DE2=BD2+EC2 , 可得MN2=FM2+NG2 , 即点M,N是线段FG的勾股分割点;(3)①先判定△BEM∽△DAM,得出
=k,进而得到FM=kBD,MN=kDE,NG=kEC,再根据DE2=BD2+EC2 , 可得MN2=FM2+NG2 , 即点M,N是线段FG的勾股分割点;(3)①先判定△BEM∽△DAM,得出 ![]() =
= ![]() ,再根据BE=
,再根据BE= ![]() BC,可得出BM=
BC,可得出BM= ![]() DM,BM=
DM,BM= ![]() BD,同理可得,DN=
BD,同理可得,DN= ![]() BD,进而得到MN=BD﹣BM﹣DN=
BD,进而得到MN=BD﹣BM﹣DN= ![]() BD,再根据MN2=BM2+ND2 , 可得M、N是线段BD的勾股分割点.②将△AND绕点A顺时针旋转,旋转角等于∠BAD,则AD旋转后与AB重合,点N旋转至点K的位置,DN=BK,∠ADN=∠ABK,连接KM,先判定△KAM≌△NAM,即可得出KM=NM,再根据点M、N是线段BD的勾股分割点,可得△KBM是直角三角形,再根据sin∠KBM=
BD,再根据MN2=BM2+ND2 , 可得M、N是线段BD的勾股分割点.②将△AND绕点A顺时针旋转,旋转角等于∠BAD,则AD旋转后与AB重合,点N旋转至点K的位置,DN=BK,∠ADN=∠ABK,连接KM,先判定△KAM≌△NAM,即可得出KM=NM,再根据点M、N是线段BD的勾股分割点,可得△KBM是直角三角形,再根据sin∠KBM= ![]() ,可得BM:MN:ND=13:12:5或BM:MN:ND=5:12:13.
,可得BM:MN:ND=13:12:5或BM:MN:ND=5:12:13.
【考点精析】通过灵活运用勾股定理的概念和图形的旋转,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素即可以解答此题.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
【题目】网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,为了解市民对售后评价的关注情况,随机采访部分市民,对采访情况制作了如下统计图表:
关注情况 | 频数 | 频率 |
A.高度关注 | 50 | b |
B.一般关注 | 120 | 0.6 |
C.不关注 | a | 0.1 |
D.不知道 | 10 | 0.05 |
(1)根据上述统计图可得此次采访的人数为人,a= , b=;
(2)根据以上信息补全条形统计图; 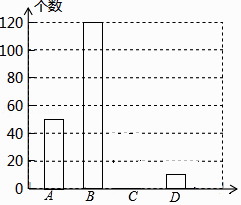
(3)根据上述采访结果,请估计在6400名市民中,高度关注售后评价的市民约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是一个非常重要的数学工具,通过它把数和数轴上的点建立起对应关系,揭示了数与点之间的内在的联系,它是“数形结合”的基础,请利用数轴解决下列问题:
(1)画出数轴,并在数轴上画出表示下列各数的点:﹣4.5,﹣2,0,1.5,3;
(2)用“>”号将(1)中各数连接起来;
(3)直接填空:数轴上表示3和表示1的两点之间的距离是 ,数轴上若A点表示的数为4,B点表示的数为﹣2,则A、B之间的距离是 .
(4)若数轴上A点表示的数为﹣3,且A、B两点间的距离为3,则B点表示的数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
![]()
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲、乙两组工作一天,商店各应付多少钱?
(2)已知甲单独完成需12天,乙单独完成需24天,单独请哪个组,商店所需费用最少?
(3)若装修完后,商店每天可赢利200元,你认为如何安排施工更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在江苏卫视《最强大脑》节目中,搭载百度大脑的小度机器人以3:1的总战绩,斩获2017年度脑王巅峰对决的晋级资格,人工智能时代已经扑面而来.
某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(﹣3![]() )﹣(﹣2
)﹣(﹣2![]() )﹣(﹣2
)﹣(﹣2![]() )﹣(+1.75)﹣(﹣1
)﹣(+1.75)﹣(﹣1![]() )
)
(2)﹣4×(﹣2![]() )﹣6×(﹣2
)﹣6×(﹣2![]() )+17×(﹣2
)+17×(﹣2![]() )﹣19
)﹣19![]() ÷
÷![]()
(3)﹣12+![]() ×[﹣22+(﹣3)2×(﹣2)+(﹣3)]÷(﹣
×[﹣22+(﹣3)2×(﹣2)+(﹣3)]÷(﹣![]() )2
)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500m高度C
处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45°.求隧道AB的长
(![]() ≈1.73).
≈1.73).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
如图①,若线段AB在数轴上,A,B点表示的数分别为a,b(b>a),则线段AB的长(点A到点B的距离)可表示为AB=b﹣a

请用上面材料中的知识解答下面的问题:
如图②,一个点从数轴上的原点开始,先向左移动1cm到达A点,再向左移动2cm到达B点,然后向右移动7cm到达C点,用1个单位长度表示1cm
(1)请你在数轴上表示出A,B,C三点的位置,并直接写出线段AC的长度;
(2)若数轴上有一点D,且AD=4cm,则点D表示的数是什么?
(3)若将点A向右移动xcm,请用代数式表示移动后的点表示的数?
(4)若点B以每秒2cm的速度向左移动至点P1,同时点A,点C分别以每秒1cm和4cm的速度向右移动至点P2,点P3,设移动时间为t秒,试探索:P3P2﹣P1P2的值是否会随着t的变化而变化?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com