
【题目】一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲、乙两组工作一天,商店各应付多少钱?
(2)已知甲单独完成需12天,乙单独完成需24天,单独请哪个组,商店所需费用最少?
(3)若装修完后,商店每天可赢利200元,你认为如何安排施工更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)
【答案】
(1)解:设:甲组工作一天商店应付x元,乙组工作一天商店付y元.
由题意得 ![]()
解得 ![]()
答:甲、乙两组工作一天,商店各应付300元和140元.
(2)解:单独请甲组需要的费用:300×12=3600元.
单独请乙组需要的费用:24×140=3360元.
答:单独请乙组需要的费用少.
(3)解:请两组同时装修,理由:
甲单独做,需费用3600元,少赢利200×12=2400元,相当于损失6000元;
乙单独做,需费用3360元,少赢利200×24=4800元,相当于损失8160元;
甲乙合作,需费用3520元,少赢利200×8=1600元,相当于损失5120元;
因为5120<6000<8160,
所以甲乙合作损失费用最少.
答:甲乙合作施工更有利于商店.
【解析】(1)本题的等量关系是:甲做8天需要的费用+乙作8天需要的费用=3520元.甲组6天需付的费用+乙做12天需付的费用=3480元,由此可得出方程组求出解.(2)根据(1)得出的甲乙每工作一天,商店需付的费用,然后分别计算出甲单独做12天需要的费用,乙单独做24天需要的费用,让两者进行比较即可.(3)本题可将每种施工方法的施工费加上施工期间商店损失的费用,然后将不同方案计算出的结果进行比较,损失最少的方案就是最有利商店的方案.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】为了鼓励市民节约用水,某市水费实行分段计费制,每户每月用水量在规定用量及以下的部分收费标准相同,超出规定用量的部分收费标准相同.例如:若规定用量为10吨,每月用水量不超过10吨按1.5元/吨收费,超出10吨的部分按2元/吨收费,则某户居民一个月用水8吨,则应缴水费:8×1.5=12(元);某户居民一个月用水13吨,则应缴水费:10×1.5+(13﹣10)×2=21(元).
表是小明家1至4月份用水量和缴纳水费情况,根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 6 | 7 | 12 | 15 |
水费(元) | 12 | 14 | 28 | 37 |
(1)该市规定用水量为 吨,规定用量内的收费标准是 元/吨,超过部分的收费标准是 元/吨.
(2)若小明家五月份用水20吨,则应缴水费 元.
(3)若小明家六月份应缴水费46元,则六月份他们家的用水量是多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知平行四边形ABCD的点A(0,﹣2)、点B(3m,4m+1)(m≠﹣1),点C(6,2),则对角线BD的最小值是( )
A. 3![]() B. 2
B. 2![]() C. 5 D. 6
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
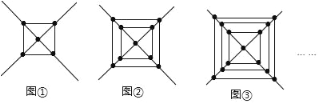
【题目】观察下列各图形中点的个数,根据其中蕴含的规律回答下列问题:
(1)图①中有 个点;图②中有 个点;图③中有 个点;
(2)请用代数式表示出第n个图形中点个数;并求第10个图形中共有多少个点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(![]() )﹣2﹣
)﹣2﹣![]() +(
+(![]() ﹣4)0﹣
﹣4)0﹣![]() cos45°.
cos45°.
【答案】1
【解析】试题分析:把原式的第一项根据负整数指数幂的意义化简,第二项根据算术平方根的定义求出9的算术平方根,第三项根据零指数公式化简,最后一项利用特殊角的三角函数值化简,合并后即可求出值.
试题解析:原式=4﹣3+1﹣![]()
=2﹣1
=1.
【题型】解答题
【结束】
16
【题目】《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙行各几何”.大意是说,已知甲、乙二人同时从同一地
点出发,甲的速度为7,乙的速度为3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲、乙各走了多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:点M,N把线段AB分割成AM、MN,NB,若以AM、MN、NB为边的三角形是一个直角三角形,则称点M、N是线段AB的勾股分割点.
(1)如图①,已知M、N是线段AB的勾股分割点,AM=6,MN=8,求NB的长;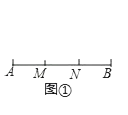
(2)如图②,在△ABC中,点D、E在边线段BC上,且BD=3,DE=5,EC=4,直线l∥BC,分别交AB、AD、AE、AC于点F、M、N、G.求证:点M,N是线段FG的勾股分割点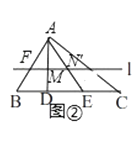
(3)在菱形ABCD中,∠ABC=β(β<90°),点E、F分别在BC、CD上,AE、AF分别交BD于点M、N.
①如图③,若BE= ![]() BC,DF=
BC,DF= ![]() CD,求证:M、N是线段BD的勾股分割点.
CD,求证:M、N是线段BD的勾股分割点.
②如图④,若∠EAF= ![]() ∠BAD,sinβ=
∠BAD,sinβ= ![]() ,当点M、N是线段AB的勾股分割点时,求BM:MN:ND的值.
,当点M、N是线段AB的勾股分割点时,求BM:MN:ND的值.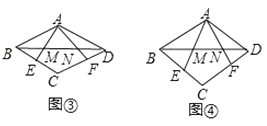
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图,在等腰直角三角形MNC中,CN=MN=![]() ,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
(1)∠NCO的度数为________;
(2)求证:△CAM为等边三角形;
(3)连接AN,求线段AN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH…添的钢管长度都与OE相等,则最多能添加这样的钢管( )根.

A. 2 B. 4 C. 5 D. 无数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com