
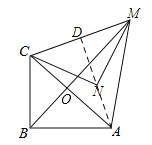
【题目】(题文)如图,在等腰直角三角形MNC中,CN=MN=![]() ,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,BM,BM交AC于点O.
(1)∠NCO的度数为________;
(2)求证:△CAM为等边三角形;
(3)连接AN,求线段AN的长.

【答案】(1)15°;(2)证明见解析;(3)![]()
【解析】(1)由旋转可得∠ACM=60°,再根据等腰直角三角形MNC中,∠MCN=45°,运用角的和差关系进行计算即可得到∠NCO的度数;
(2)根据有一个角是60°的等腰三角形是等边三角形进行证明即可;
(3)根据△MNC是等腰直角三角形,△ACM是等边三角形,判定△ACN≌△AMN,再根据Rt△ACD中,AD=![]() CD=
CD=![]() ,等腰Rt△MNC中,DN=
,等腰Rt△MNC中,DN=![]() CM=1,即可得到AN=AD﹣ND=
CM=1,即可得到AN=AD﹣ND=![]() ﹣1.
﹣1.
(1)由旋转可得∠ACM=60°.
又∵等腰直角三角形MNC中,∠MCN=45°,∴∠NCO=60°﹣45°=15°;
故答案为:15°;
(2)∵∠ACM=60°,CM=CA,∴△CAM为等边三角形;
(3)连接AN并延长,交CM于D.
∵△MNC是等腰直角三角形,△ACM是等边三角形,∴NC=NM=![]() ,CM=2,AC=AM=2.在△ACN和△AMN中,∵
,CM=2,AC=AM=2.在△ACN和△AMN中,∵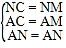 ,∴△ACN≌△AMN(SSS),∴∠CAN=∠MAN,∴AD⊥CM,CD=
,∴△ACN≌△AMN(SSS),∴∠CAN=∠MAN,∴AD⊥CM,CD=![]() CM=1,∴Rt△ACD中,AD=
CM=1,∴Rt△ACD中,AD=![]() CD=
CD=![]() ,等腰Rt△MNC中,DN=
,等腰Rt△MNC中,DN=![]() CM=1,∴AN=AD﹣ND=
CM=1,∴AN=AD﹣ND=![]() ﹣1.
﹣1.


科目:初中数学 来源: 题型:
【题目】煤气公司一工人检修一条长540米的煤气管道,计划用若干小时完成,在实际检修过程中,每小时检修的管道长度是原计划的1.5倍,结果提前3小时完成任务,求该工人原计划每小时检修煤气管道多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣20+8﹣(﹣1)+(﹣4)
(2)![]() ×(﹣
×(﹣![]() )2÷(﹣0.5)3
)2÷(﹣0.5)3
(3)4﹣6÷(﹣2)×(﹣![]() )
)
(4)(﹣36)×(﹣![]() +
+![]() ﹣
﹣![]() )
)
(5)(﹣2)2×0.5﹣(﹣1.6)2÷(﹣2)3
(6)﹣14÷(﹣4)﹣(﹣![]() )2×(﹣3)+|(﹣1)2﹣2|
)2×(﹣3)+|(﹣1)2﹣2|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲、乙两组工作一天,商店各应付多少钱?
(2)已知甲单独完成需12天,乙单独完成需24天,单独请哪个组,商店所需费用最少?
(3)若装修完后,商店每天可赢利200元,你认为如何安排施工更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(﹣3![]() )﹣(﹣2
)﹣(﹣2![]() )﹣(﹣2
)﹣(﹣2![]() )﹣(+1.75)﹣(﹣1
)﹣(+1.75)﹣(﹣1![]() )
)
(2)﹣4×(﹣2![]() )﹣6×(﹣2
)﹣6×(﹣2![]() )+17×(﹣2
)+17×(﹣2![]() )﹣19
)﹣19![]() ÷
÷![]()
(3)﹣12+![]() ×[﹣22+(﹣3)2×(﹣2)+(﹣3)]÷(﹣
×[﹣22+(﹣3)2×(﹣2)+(﹣3)]÷(﹣![]() )2
)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由若干边长为1的小正方形拼成一系列“L”形图案(如图1).
(1)当“L”形由7个正方形组成时,其周长为;
(2)如图2,过格点D作直线EF,分别交AB,AC于点E,F.
①试说明AEAF=AE+AF;
②若“L”形由n个正方形组成时,EF将“L”形分割开,直线上方的面积为整个“L”形面积的一半,试求n的取值范围以及此时线段EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com