
【题目】在平面直角坐标系中,已知平行四边形ABCD的点A(0,﹣2)、点B(3m,4m+1)(m≠﹣1),点C(6,2),则对角线BD的最小值是( )
A. 3![]() B. 2
B. 2![]() C. 5 D. 6
C. 5 D. 6
【答案】D
【解析】分析:先根据B(3m,4m+1),可知B在直线y=![]() x+1上,所以当BD⊥直线y=
x+1上,所以当BD⊥直线y=![]() x+1时,BD最小,找一等量关系列关于m的方程,作辅助线:过B作BH⊥x轴于H,则BH=4m+1,利用三角形相似得BH2=EHFH,列等式求m的值,得BD的长即可.
x+1时,BD最小,找一等量关系列关于m的方程,作辅助线:过B作BH⊥x轴于H,则BH=4m+1,利用三角形相似得BH2=EHFH,列等式求m的值,得BD的长即可.
详解:如图,
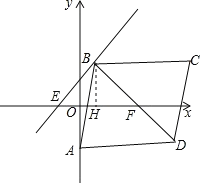
∵点B(3m,4m+1),
∴令![]() ,
,
∴y=![]() x+1,
x+1,
∴B在直线y=![]() x+1上,
x+1上,
∴当BD⊥直线y=![]() x+1时,BD最小,
x+1时,BD最小,
过B作BH⊥x轴于H,则BH=4m+1,
∵BE在直线y=![]() x+1上,且点E在x轴上,
x+1上,且点E在x轴上,
∴E(![]() ,0),G(0,1)
,0),G(0,1)
∵F是AC的中点
∵A(0,2),点C(6,2),
∴F(3,0)
在Rt△BEF中,
∵BH2=EHFH,
∴(4m+1)2=(3m+![]() )(33m),
)(33m),
解得:m1=![]() (舍),m2=
(舍),m2=![]() ,
,
∴B(![]() ,
,![]() ),
),
∴BD=2BF=2×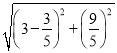 =6,
=6,
则对角线BD的最小值是6;
故答案为:6.


科目:初中数学 来源: 题型:
【题目】将5个完全相同的小球分装在甲、乙两个不透明的口袋中.甲袋中有3个球,分别标有数字2,3,4;乙袋中有2个球,分别标有数字2,4.从甲、乙两个口袋中各随机摸出一个球.
(1)用列表法或画树状图法,求摸出的两个球上数字之和为5的概率.
(2)摸出的两个球上数字之和为多少时的概率最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】煤气公司一工人检修一条长540米的煤气管道,计划用若干小时完成,在实际检修过程中,每小时检修的管道长度是原计划的1.5倍,结果提前3小时完成任务,求该工人原计划每小时检修煤气管道多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“ 六一”儿童节前夕,蕲黄县教育局准备给留守儿童赠送一批学习用品,先对浠泉镇浠泉小学的留守儿童人数进行抽样统计,发现各班留守儿童人数分别为6 名,7 名,8 名,10 名,12 名这五种情形,并将统计结果绘制成了如图所示的两幅不完整的统计图.
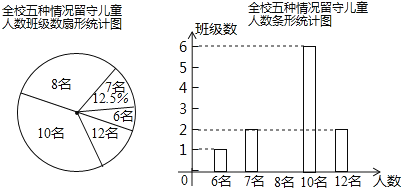
请根据上述统计图,解答下列问题:
(1)该校有多少个班级?并补全条形统计图;
(2)该校平均每班有多少名留守儿童?留守儿童人数的众数是多少?
(3)若该镇所有小学共有60 个教学班,请根据样本数据,估计该镇小学生中,共有多少名留守儿童.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,圆D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.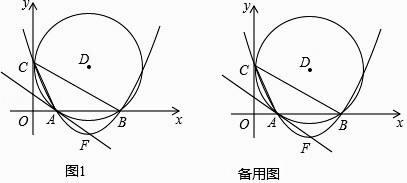
(1)D点的坐标是 , 圆的半径为;
(2)求经过C、A、B三点的抛物线所对应的函数关系式;
(3)设抛物线的顶点为F,试证明直线AF与圆D相切;
(4)在x轴下方的抛物线上,是否存在一点N,使△CBN面积最大,最大面积是多少?并求出N点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是一个非常重要的数学工具,通过它把数和数轴上的点建立起对应关系,揭示了数与点之间的内在的联系,它是“数形结合”的基础,请利用数轴解决下列问题:
(1)画出数轴,并在数轴上画出表示下列各数的点:﹣4.5,﹣2,0,1.5,3;
(2)用“>”号将(1)中各数连接起来;
(3)直接填空:数轴上表示3和表示1的两点之间的距离是 ,数轴上若A点表示的数为4,B点表示的数为﹣2,则A、B之间的距离是 .
(4)若数轴上A点表示的数为﹣3,且A、B两点间的距离为3,则B点表示的数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣20+8﹣(﹣1)+(﹣4)
(2)![]() ×(﹣
×(﹣![]() )2÷(﹣0.5)3
)2÷(﹣0.5)3
(3)4﹣6÷(﹣2)×(﹣![]() )
)
(4)(﹣36)×(﹣![]() +
+![]() ﹣
﹣![]() )
)
(5)(﹣2)2×0.5﹣(﹣1.6)2÷(﹣2)3
(6)﹣14÷(﹣4)﹣(﹣![]() )2×(﹣3)+|(﹣1)2﹣2|
)2×(﹣3)+|(﹣1)2﹣2|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:
(1)甲、乙两组工作一天,商店各应付多少钱?
(2)已知甲单独完成需12天,乙单独完成需24天,单独请哪个组,商店所需费用最少?
(3)若装修完后,商店每天可赢利200元,你认为如何安排施工更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com