
【题目】如图1,在平面直角坐标系中,圆D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.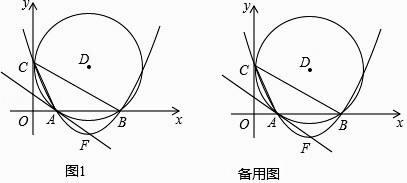
(1)D点的坐标是 , 圆的半径为;
(2)求经过C、A、B三点的抛物线所对应的函数关系式;
(3)设抛物线的顶点为F,试证明直线AF与圆D相切;
(4)在x轴下方的抛物线上,是否存在一点N,使△CBN面积最大,最大面积是多少?并求出N点坐标.
【答案】
(1)(5,4);5
(2)
解:如图1所示:
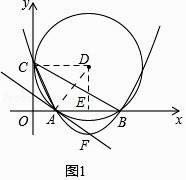
∵D(5,4),
∴E(5,0).
∴A(2,0)、B(8,0).
设抛物线的解析式为y=a(x﹣2)(x﹣8),将点C的坐标代入得:16a=4,解得:a= ![]() ,
,
∴抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x+4.
x+4.
(3)
解:∵y= ![]() x2﹣
x2﹣ ![]() x+4,
x+4,
∴抛物线的顶点坐标F(5,﹣ ![]() ).
).
∴DF=4+ ![]() =
= ![]() ,AF=
,AF= ![]() =
= ![]() .
.
又∵AD=5.
∴AD2+AF2=DF2,
∴△DAF为直角三角形.
∴∠DAF=90°.
∴AF是⊙D的切线.
(4)
解:如图2所示:过点N作NP∥y轴,交BC与点P.
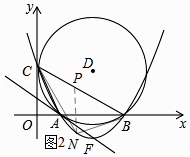
设BC的解析式为y=kx+4,将点B的坐标代入得:8k+4=0,解得k=﹣ ![]() .
.
∴BC的解析式为y=﹣ ![]() x+4.
x+4.
设N点坐标(a, ![]() a2﹣
a2﹣ ![]() a+4),则点P坐标为(a,﹣
a+4),则点P坐标为(a,﹣ ![]() a+4).
a+4).
∴NP=﹣ ![]() a+4﹣(
a+4﹣( ![]() a2﹣
a2﹣ ![]() a+4)=﹣
a+4)=﹣ ![]() a2+2a.
a2+2a.
∴S△ABC=S△CPN+S△PBN= ![]() ×BO×PN=
×BO×PN= ![]() ×8×(﹣
×8×(﹣ ![]() a2+2a)=﹣(a﹣4)2+16.
a2+2a)=﹣(a﹣4)2+16.
∴当a=4时,S△ABC最大,最大值为16,此时,N(4,﹣2).
【解析】解:(1)连接CD,过点D作DE⊥AB,垂足为E,连接AD.
∵DE⊥AB,
∴AE= ![]() AB=3.
AB=3.
∵⊙D与y轴相切,
∴DC⊥y轴.
∵∠COE=∠OED=∠OCD=90°,
∴四边形OCDE为矩形.
∴OC=DE.
∵C(0,4),
∴DE=4.
在Rt△AED中,AD= ![]() =5.
=5.
∴⊙D的半径为5.
∴D(5,4).
所以答案是:(5,4),5.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图是小明用七巧板拼出的图案.
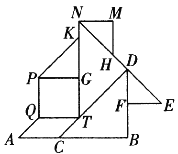
(1)请赋予该图形一个积极的含义;
(2)请你找出图中2组平行线段和2对互相垂直的线段,用符号表示它们;
(3)找出图中一个锐角、一个钝角和一个直角,将它们表示出来,并指出它们的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,六边形ABCDEF的内角都相等,∠DAB=60°,AB=DE,则下列结论成立的个数是( )
①AB∥DE;②EF∥AD∥BC;③AF=CD;④四边形ACDF是平行四边形;⑤六边形ABCDEF既是中心对称图形,又是轴对称图形.

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解中学生获取信息的主要渠道,设置“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项)的调查问卷,先随机抽取50名中学生进行该问卷调查,根据调查的结果绘制条形图如图,该调查的方式和图中a的值分别是( )

A. 抽样调查,24 B. 普查,24 C. 抽样调查,26 D. 普查,26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图.
(1)求证:△ADC≌△CEB;
(2)从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).
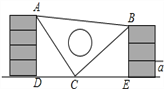
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知平行四边形ABCD的点A(0,﹣2)、点B(3m,4m+1)(m≠﹣1),点C(6,2),则对角线BD的最小值是( )
A. 3![]() B. 2
B. 2![]() C. 5 D. 6
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学七年级四班的同学在体检中测量了自己的身高,并求出了该班同学的平均身高.
(1)下表给出了该班5名同学的身高情况(单位:cm),试完成该表,并求出该班同学的平均身高.
姓名 | 刘杰 | 刘涛 | 李明 | 张春 | 刘建 |
身高 | 161 |
|
| 165 | 155 |
身高与全班同 学平均身高差 | +3 | ﹣1 | 0 |
|
|
(2)谁最高?谁最矮?
(3)计算这5名同学的平均身高是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(![]() )﹣2﹣
)﹣2﹣![]() +(
+(![]() ﹣4)0﹣
﹣4)0﹣![]() cos45°.
cos45°.
【答案】1
【解析】试题分析:把原式的第一项根据负整数指数幂的意义化简,第二项根据算术平方根的定义求出9的算术平方根,第三项根据零指数公式化简,最后一项利用特殊角的三角函数值化简,合并后即可求出值.
试题解析:原式=4﹣3+1﹣![]()
=2﹣1
=1.
【题型】解答题
【结束】
16
【题目】《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙行各几何”.大意是说,已知甲、乙二人同时从同一地
点出发,甲的速度为7,乙的速度为3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲、乙各走了多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E. 
(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com