
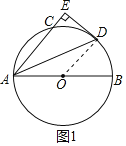
【题目】如图,AB是![]() 的直径,AC为弦,
的直径,AC为弦,![]() 的平分线交
的平分线交![]() 于点D,过点D的切线交AC的延长线于点E.
于点D,过点D的切线交AC的延长线于点E.
求证:![]() ;
;
![]() .
.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)连接OD,根据等腰三角形的性质结合角平分线的性质可得出∠CAD=∠ODA,利用“内错角相等,两直线平行”可得出AE//OD,结合切线的性质即可证出DE⊥AE;
(2)过点D作DM⊥AB于点M,连接CD、DB,根据角平分线的性质可得出DE=DM,结合AD=AD、∠AED=∠AMD=90°即可证出△DAE≌△DAM(SAS),根据全等三角形的性质可得出AE=AM,由∠EAD=∠MAD可得出![]() ,进而可得出CD=BD,结合DE=DM可证出Rt△DEC≌Rt△DMB(HL),根据全等三角形的性质可得出CE=BM,结合AB=AM+BM即可证出AE+CE=AB.
,进而可得出CD=BD,结合DE=DM可证出Rt△DEC≌Rt△DMB(HL),根据全等三角形的性质可得出CE=BM,结合AB=AM+BM即可证出AE+CE=AB.
![]() 连接OD,如图1所示,
连接OD,如图1所示,
![]() ,AD平分
,AD平分![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的切线,
的切线,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 过点D作
过点D作![]() 于点M,连接CD、DB,如图2所示,
于点M,连接CD、DB,如图2所示,

![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,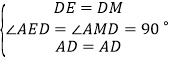 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() .
.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】某校为提升硬件设施,决定采购80台电脑,现有A,B两种型号的电脑可供选择.已知每台A型电脑比B型的贵2000元,2台A型电脑与3台B型电脑共需24000元.
(1)分别求A,B两种型号电脑的单价;
(2)若A,B两种型号电脑的采购总价不高于38万元,则A型电脑最多采购多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在![]() 中,C是BP边上一点,PA是
中,C是BP边上一点,PA是![]() 的切线,
的切线,![]() 是
是![]() 的外接圆,AD是
的外接圆,AD是![]() 的直径,且交BP于点E.
的直径,且交BP于点E.
![]() 求证:
求证:![]() ;
;
![]() 过点C作
过点C作![]() ,垂足为点F,延长CF交AB于点G,若
,垂足为点F,延长CF交AB于点G,若![]() ,AF:
,AF:![]() :3,
:3,![]()
①求CF的长;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ACB中,∠ACB=90°,∠A=75°,点D是AB的中点.将△ACD沿CD翻折得到△A′CD,连接A′B.

(1)求证:CD∥A′B;
(2)若AB=4,求A′B2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陈杰骑自行车去上学,当他以往常的速度骑了一段路时,忽然想起要买某本书,于是又折回到刚经过的一家书店,买到书后继续赶去学校.以下是他本次上学的路程与所用时间的关系示意图.根据图中提供的信息回答下列问题:
(1)陈杰家到学校的距离是多少米?书店到学校的距离是多少米?
(2)陈杰在书店停留了多少分钟?本次上学途中,陈杰一共行驶了多少米?
(3)在整个上学的途中哪个时间段陈杰骑车速度最快?最快的速度是多少米?
(4)如果陈杰不买书,以往常的速度去学校,需要多少分钟?本次上学比往常多用多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了帮助本市一名患“白血病”的高中生,某班15名同学积极捐款,他们捐款数额如下表:
捐款的数额(单位:元) | 5 | 10 | 20 | 50 | 100 |
人数(单位:个) | 2 | 4 | 5 | 3 | 1 |
关于这15名同学所捐款的数额,下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境,某企业决定购买10台污水处理设备;现有A、B两种型号的设备,其中每台的价格、月处理污水量及年消耗费如下表:
A型 | B型 | |
价格(万元/台) | 12 | 10 |
处理污水量(吨/月) | 240 | 200 |
年消耗费(万元/台) | 1 | 1 |
经预算,该企业购买设备的资金不高于105万元。
(1) 请你设计该企业有几种购买方案;
(2)若该企业每月产生的污水量为2040吨,为了节约资金,应选择哪种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
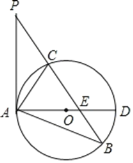
【题目】(1)如图1,∠MAN=90°,射线AE在这个角的内部,点B、C分别在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D.求证:△ABD≌△CAF;
(2)如图2,点B、C分别在∠MAN的边AM、AN上,点E、F都在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC,且∠1=∠2=∠BAC.求证:△ABE≌△CAF;
(3)如图3,在△ABC中,AB=AC,AB>BC.点D在边BC上,CD=2BD,点E、F在线段AD上,∠1=∠2=∠BAC.若△ABC的面积为15,求△ACF与△BDE的面积之和.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为∠BAC的外角平分线上一点,并且满足BD=CD,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①![]() ;②∠DBC=∠DCB;③CE=AB+AE④∠BDC=∠BAC,其中正确的结论有( )
;②∠DBC=∠DCB;③CE=AB+AE④∠BDC=∠BAC,其中正确的结论有( )
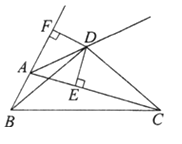
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com