
【题目】如图,一次函数![]() 的图象分别与
的图象分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() ,以线段
,以线段![]() 为边在第一象限内作等腰直角三角形
为边在第一象限内作等腰直角三角形![]() ,使
,使![]() .
.
(1)分别求点![]() 的坐标;
的坐标;
(2)在![]() 轴上求一点
轴上求一点![]() ,使它到
,使它到![]() 两点的距离之和最小.
两点的距离之和最小.

【答案】(1) B的坐标是(0,2),C的坐标是(5,3);(2) P(2,0).
【解析】
(1)先根据一次函数的解析式求出A、B两点的坐标,再作CD⊥x轴于点D,由全等三角形的判定定理可得出△ABO≌△CAD,由全等三角形的性质可知OA=CD,故可得出C点坐标;
(2)求得B点关于x轴的对称点B'的坐标,连接B'C与x轴的交点即为所求的P点,由B'、C坐标可求得直线B'C的解析式,则可求得P点坐标.
解:∵一次函数![]() 中,令x=0得:y=2;
中,令x=0得:y=2;
令y=0,解得x=3.
∴B的坐标是(0,2),A的坐标是(3,0).
作CD⊥x轴于点D.
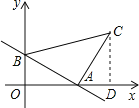
∵∠BAC=90°,
∴∠OAB+∠CAD=90°,
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO,
又∵AB=AC,∠BOA=∠CDA=90°,
∴△ABO≌△CAD(AAS),
∴AD=OB=2,CD=OA=3,OD=OA+AD=5.
则C的坐标是(5,3).
(2)如图,作点B关于x轴的对称点B',连接CB'交x轴于P,此时PB+PC的值最小.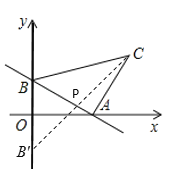
∵B(0,2),C(5,3)
∴B'(0,-2),
设直线C B'的解析式为y=kx+b,
把(0,-2) (5,3)代入y=kx+b中,
可得:![]() ,
,
解得:![]() ,
,
∴直线CB'的解析式为y=x-2,
令y=0,得到x=2,
∴P(2,0).


 新课标同步训练系列答案
新课标同步训练系列答案科目:初中数学 来源: 题型:
【题目】(1)请用两种不同的方法列代数式表示图中阴影部分的面积.

方法①_________________;
方法②_________________;
(2)根据(1)写出一个等式________________;
(3)若![]() ,
,![]() .
.
①求![]() 的值。
的值。
②![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是△ABC的内心,AE的延长线交BC于点F,交△ABC的外接圆⊙O于点D,连接BD,过点D作直线DM,使∠BDM=∠DAC. (Ⅰ)求证:直线DM是⊙O的切线;
(Ⅱ)求证:DE2=DFDA.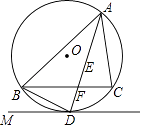
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的顶点均在边长为1的小正方形网络中的格点上,如图,建立平面直角坐标系,点B在x轴上.
(1)在图中画出△ABC关于x轴对称的△A’B’C’,连接AA’,求证:△AA’C≌△A’AC’;
(2)请在y轴上画点P,使得PB+PC最短.(保留作图痕迹,不写画法)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,∠ABE与∠CDE的角平分线相交于点F,若∠F=125°,则∠E的度数为( )

A. 110° B. 120° C. 115° D. 105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形入手.先计算下列各式的值:
(1)(x﹣1)(x+1)= ;
(2)(x﹣1)(x2+x+1)= ;
(3)(x﹣1)(x3+x2+x+1)= ;
由此我们可以得到(x﹣1)(x99+x98+…+x+1)= ;
请你利用上面的结论,完成下面两题的计算:
(1)299+298+…+2+1;
(2)(﹣3)50+(﹣3)49+…+(﹣3)+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )
A.29°
B.32°
C.42°
D.58°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com