Question

【题目】在中， 为直线上一动点（点不与、重合）.以为边作正方形，连接.

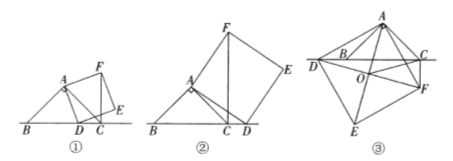
（1）如图①,当点在线段上时，求证:①;②.

（2）如图②,当点在线段的延长线上时，其他条件不变，请直接写出、、三条线段之间的关系.

（3）如图③,当点在线段的反向延长线上时，且点、分别在直线的两侧，其他条件不变①请直接写出、、三条线段之间的关系;②若连接正方形对角线、,交点为，连接，探究的形状，并说明理由.

Answer 1

【答案】（1）、证明过程见解析；（2）、CF=BC+CD，证明过程见解析；（3）、CF=CD-BC；△AOC是等腰三角形，理由见解析

【解析】

试题分析：（1）、①、根据等腰直角的性质得出∠ABC=∠ACB=45°，从而得出四边形ADEF是正方形，根据∠BAC=∠BAD+∠DAC=90°，∠DAF=∠CAF+∠DAC=90°得出∠BAD=∠CAF，从而得出△BAD和△CAF全等，则∠ACF=∠ABD=45°，从而得出垂直；②、根据 全等得出BD=CF，从而得出结论；（2）、根据（1）的证法的采购员BD=CF，得出CF=BC+CD；（3）、①、根据（1）的证法得出BD=CF，从而得出CF=CD-BC；②、∠BAC=90°，AB=AC得出∠ABD=135°，根据四边形ADEF是正方形得出∠BAC=∠BAF+∠CAF=90°，∠DAF=∠BAD+∠BAF=90°，从而得出△BAD和△CAF全等，则∠ACF=135°，从而得出∠FCD=∠ACF-∠ACB=90°，得出△FCD为直角三角形，根据正方形的性质得出OC=OA，从而说明△FCD为等腰直角三角形.

试题解析：（1）、①、∵∠BAC=90°，AB=AC， ∴∠ABC=∠ACB=45°， ∵四边形ADEF是正方形，

∴AD=AF，∠DAF=90°， ∵∠BAC=∠BAD+∠DAC=90°，∠DAF=∠CAF+∠DAC=90°， ∴∠BAD=∠CAF，

在△BAD和△CAF中， AB=AC ∠BAD=∠CAF AD=AF ∴△BAD≌△CAF（SAS），

∴∠ACF=∠ABD=45°， ∴∠ACF+∠ACB=90°， ∴BD⊥CF；

②、由①△BAD≌△CAF可得BD=CF， ∵BD=BC-CD， ∴CF=BC-CD；

（2）、与（1）同理可得BD=CF， 所以，CF=BC+CD；

（3）、①、与（1）同理可得，BD=CF， 所以，CF=CD-BC；

②∵∠BAC=90°，AB=AC， ∴∠ABC=∠ACB=45°， 则∠ABD=180°-45°=135°，

∵四边形ADEF是正方形， ∴AD=AF，∠DAF=90° ∵∠BAC=∠BAF+∠CAF=90°，∠DAF=∠BAD+∠BAF=90°，

∴∠BAD=∠CAF， 在△BAD和△CAF中，AB=AC ∠BAD=∠CAF AD=AF ∴△BAD≌△CAF（SAS），

∴∠ACF=∠ABD=180°-45°=135°， ∴∠FCD=∠ACF-∠ACB=90°，则△FCD为直角三角形，

∵正方形ADEF中，O为DF中点， ∴OC=DF ∵在正方形ADEF中，OA=AEAE=DF， ∴OC=OA，

∴△AOC是等腰三角形