
【题目】已知四边形ABCD中,AB=AD,AB⊥AD,连接AC,过点A作AE⊥AC,且使AE=AC,连接BE,过A作AH⊥CD于H交BE于F.

(1)如图1,当E在CD的延长线上时,求证:①△ABC≌△ADE;②BF=EF;
(2)如图2,当E不在CD的延长线上时,BF=EF还成立吗?请证明你的结论.
【答案】(1)详见解析;(2)结论仍然成立,理由详见解析.
【解析】
试题分析:(1)①根据已知条件,利用SAS即可判定△ABC≌△ADE;②易证BC∥FH和CH=HE,根据平行线分线段成比例定理可证得BF=EF.(2)过E作MN⊥AH,交BA、CD延长线于M、N,,利用ASA证明△MAE≌△DAC,得AD=AM,根据等量代换得AB=AM,根据②同理得出结论.
试题解析:证明:(1)①如图1,
∵AB⊥AD,AE⊥AC,
∴∠BAD=90°,∠CAE=90°,
∴∠1=∠2,
在△ABC和△ADE中,
∵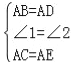
∴△ABC≌△ADE(SAS);
②如图1,
∵△ABC≌△ADE,
∴∠AEC=∠3,
在Rt△ACE中,∠ACE+∠AEC=90°,
∴∠BCE=90°,
∵AH⊥CD,AE=AC,
∴CH=HE,
∵∠AHE=∠BCE=90°,
∴BC∥FH,
∴![]() =1,
=1,
∴BF=EF;
(2)结论仍然成立,理由是:
如图2所示,过E作MN⊥AH,交BA、CD延长线于M、N,
∵∠CAE=90°,∠BAD=90°,
∴∠1+∠2=90°,∠1+∠CAD=90°,
∴∠2=∠CAD,
∵MN∥AH,
∴∠3=∠HAE,
∵∠ACH+∠CAH=90°,∠CAH+∠HAE=90°,
∴∠ACH=∠HAE,
∴∠3=∠ACH,
在△MAE和△DAC中,
∵
∴△MAE≌△DAC(ASA),
∴AM=AD,
∵AB=AD,
∴AB=AM,
∵AF∥ME,
∴![]() =1,
=1,
∴BF=EF.


科目:初中数学 来源: 题型:
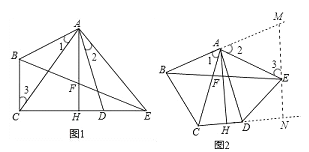
【题目】已知,如图2菱形ABCD四个顶点都在坐标轴上,对角线AC、BD交于原点O,DF垂直AB交AC于点G,反比例函数![]() ,经过线段DC的中点E,若BD=4,则AG的长为( )
,经过线段DC的中点E,若BD=4,则AG的长为( )

A.![]() B.
B.![]() +2 C.2
+2 C.2![]() +1 D.
+1 D.![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】股市规定:股票每天的涨、跌幅均不超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停.若一支股票某天跌停,之后两天时间又涨回到原价,若这两天此股票股价的平均增长率为x,则x满足的方程是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
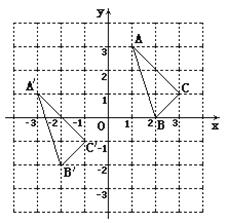
【题目】△ A B C与![]() 在平面直角坐标系中的位置如图.
在平面直角坐标系中的位置如图.
(1)分别写出下列各点的坐标: ![]() ______ ;
______ ; ![]() _______ ;
_______ ; ![]() _______ ;
_______ ;
(2)说明![]() 由△ A B C经过怎样的平移得到? ________________________________.
由△ A B C经过怎样的平移得到? ________________________________.
(3)若点![]() (
(![]() ,
, ![]() )是△ A B C内部一点,则平移后
)是△ A B C内部一点,则平移后![]() 内的对应点
内的对应点![]() 的坐标为 ________ ;
的坐标为 ________ ;
(4)求△ A B C的面积..
查看答案和解析>>
科目:初中数学 来源: 题型:
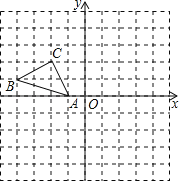
【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
(1)作出△ABC绕点A逆时针旋转90°的△AB1C1,再作出△AB1C1关于原点O成中心对称的△A1B2C2.
(2)点B1的坐标为 ,点C2的坐标为 .
(3)△ABC经过怎样的旋转可直接得到△A1B2C2, .
查看答案和解析>>
科目:初中数学 来源: 题型:
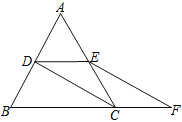
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=![]() BC,连结CD和EF.
BC,连结CD和EF.
(1)求证:四边形CDEF是平行四边形;
(2)求四边形BDEF的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com