
【题目】如图,在△ABC中,点E在线段AB上,点D在射线CB上,且ED=EC,将△BCE绕点C顺时针旋转60°至△ACF(点B、E的对应点分别为点A、F),连接EF.
(1)求证:AE=DB;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对线段长度之和等于AB的长.

【答案】(1)详见解析;(2)AE+BE=AB;BD+BE=AB;AE+AF=AB;BD+AF=AB.
【解析】
试题分析:(1)利用旋转的性质得AC=BC,∠BCA=60°,则可判断△ABC为等边三角形,过点E做EG∥AC交BC于点G,如图,则△EBG为等边三角形,所以EG=BE=BG,∠EBG=∠EGB=60°,则∠EBD=∠EGC=120°,接下来证明△BDE≌△GCE得到BD=GC,然后利用等线段代换可得到AE=DB;(2)利用BD=AE,BE=BC=CE=EF等线段代换易得四对线段,使每对线段长度之和等于AB的长.
试题解析: (1)∵△BCE绕点C顺时针旋转60°至△ACF,
∴AC=BC,∠BCA=60°,
∴△ABC为等边三角形,
过点E做EG∥AC交BC于点G,如图,
∴△EBG为等边三角形,
∴EG=BE=BG,∠EBG=∠EGB=60°,
∴∠EBD=∠EGC=120°,
∵ED=EC
∴∠D=∠ECD,
在△BDE和△GCE中
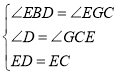 ,
,
∴△BDE≌△GCE,
∴BD=GC,
∵△ABC为等边三角形,
∴AB=BC,
∴AB﹣BE=BC﹣BG,
∴AE=CG,
∴AE=DB;
(2)AE+BE=AB;BD+BE=AB;AE+AF=AB;BD+AF=AB.



科目:初中数学 来源: 题型:
【题目】小明有五张写着不同数字的卡片,请你按要求抽出卡片,完成下列问题 ![]()
(1)从中抽出2张卡片,使这两张卡片上数字乘积最大,最大值是;
(2)从中抽出2张卡片,使这两张卡片上数字相除的商最小,最小值是;
(3)从中抽出4张卡片,用学过的运算方法,使结果为24,请你写出运算式子(至少写出两种).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值.
(1)(a–b)2+b(a–b),其中a=2,b=–![]() .
.
(2)![]() ,其中
,其中![]() ,b=-1.
,b=-1.
(3)(3x+2)(3x-2)-5x(x-1)-(2x-1)2,其中x=-![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与ECGF是两个边长分别为a,b的正方形,写出用a,b表示阴影部分面积的代数式,并计算当a=4cm,b=6cm时,阴影部分的面积. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com