
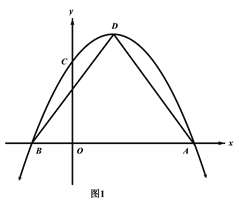
【题目】如图1,抛物线![]() 与x轴相交于A,B两点(点A在点B的右侧),与y轴交于点C,点D是抛物线的顶点,连接AD、BD.
与x轴相交于A,B两点(点A在点B的右侧),与y轴交于点C,点D是抛物线的顶点,连接AD、BD.
![]() 求△ABD的面积;
求△ABD的面积;
![]() 如图2,连接AC、BC,若点P是直线AC上方抛物线上一动点,过P作PE//BC交AC于点E,作PQ//y轴交AC于点Q,当△PQE周长最大时,将△PQE沿着直线AC平移,记移动中的△PQE为
如图2,连接AC、BC,若点P是直线AC上方抛物线上一动点,过P作PE//BC交AC于点E,作PQ//y轴交AC于点Q,当△PQE周长最大时,将△PQE沿着直线AC平移,记移动中的△PQE为![]() ,连接
,连接![]() ,求△PQE的周长的最大值及
,求△PQE的周长的最大值及![]() 的最小值;
的最小值;
![]() 如图3,点G为x轴正半轴上一点,且OG=OC,连接CG,过G作GH⊥AC于点H,将△CGH绕点O顺时针旋转
如图3,点G为x轴正半轴上一点,且OG=OC,连接CG,过G作GH⊥AC于点H,将△CGH绕点O顺时针旋转![]() (
(![]() ),记旋转中的△CGH为
),记旋转中的△CGH为![]() ,在旋转过程中,直线
,在旋转过程中,直线![]() ,
,![]() 分别与直线AC交于点M,N,
分别与直线AC交于点M,N, ![]() 能否成为等腰三角形?若能直接写出所有满足条件的
能否成为等腰三角形?若能直接写出所有满足条件的![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.


科目:初中数学 来源: 题型:
【题目】为了解长沙市七年级学生身体素质,从全市七年级学生中随机抽取部分学生进行了一次体育考试科目的测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试记录绘成如下两幅完全不同的统计图.请根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生数是________;
(2)图1中![]() 的度数是________;把图2条形统计图补充完成;
的度数是________;把图2条形统计图补充完成;
(3)长沙市某区七年级共有9800名学生,如果全部参加这次体育科目测试,请估计不及格的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
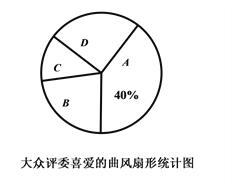
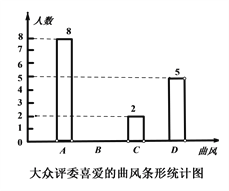
【题目】春雨初歇,绿意葱茏,重庆南开(融侨)中学初2020级举行了“春天的赞礼”为主题的合唱比赛,各班演唱歌曲的曲风有:青春舞曲、经典名曲、动漫神曲、励志金曲四种类型,为了了解同学们对各种曲风的喜爱程度。校学生处对大众评委喜爱的歌曲曲风进行了调查,(A—喜爱青春舞曲、B—喜爱经典名曲、C—喜爱动漫神曲、D—喜爱励志金曲),先根据调查得到如下图不完整的统计图,请结合图中信息完成下列问题:
![]() 扇形统计图中“C—喜爱动漫神曲”对应扇形圆心角为【1】度,并补全条形统计图.
扇形统计图中“C—喜爱动漫神曲”对应扇形圆心角为【1】度,并补全条形统计图.
![]() 在此次比赛中,甲班演唱的《四季问候》和乙班演唱的《东方之珠》获得一等奖,《司机问候》由2名男生和2名女生领唱,《东方之珠》由1名男生和2名女生领唱,校学生处打算分别从这两首歌曲的领唱中任意选取1名同学参加校合唱团,请用画树状图或列表的方法求出恰好选到1名男生和1名女生的概率.
在此次比赛中,甲班演唱的《四季问候》和乙班演唱的《东方之珠》获得一等奖,《司机问候》由2名男生和2名女生领唱,《东方之珠》由1名男生和2名女生领唱,校学生处打算分别从这两首歌曲的领唱中任意选取1名同学参加校合唱团,请用画树状图或列表的方法求出恰好选到1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图1中以格点为顶点画一个面积为10的正方形;
(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、![]() 、
、![]() ;
;
(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,0),B(0,2),以AB为边在第一象限内作正方形ABCD,直线CD与y轴交于点G,再以DG为边在第一象限内作正方形DEFG,若反比例函数![]() 的图像经过点E,则k的值是 ( )
的图像经过点E,则k的值是 ( )

(A)33 (B)34 (C)35 (D)36
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,①四边形ABCD是平行四边形,线段EF分别交AD、AC、BC于点E、O、F,②EF⊥AC,③AO=CO.
(1)求证:四边形AFCE是平行四边形;

(2)在本题①②③三个已知条件中,去掉一个条件,(1)的结论依然成立,这个条件是 (直接写出这个条件的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆汽车分别在相距180千米的A、B两地相向而行,甲车每小时比乙车每小时快20千米,甲车在乙车出发2小时后出发,甲车出发1小时两车相遇。
(1)求甲、乙两车的速度各是多少?
(2)甲、乙两车各自到达目的地后都立即返回,问甲车从A地出发多长时间甲、乙两车 相距20千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,E为AB的中点.

(1)求证:△ADC∽△ACB;
(2)CE与AD有怎样的位置关系?试说明理由;
(3)若AD=4,AB=6,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com