【题目】如图,
中
分别平分
则
的度数为（ ）
A.
B.
C.
D.
【答案】C
【解析】
先根据角平分线的定义得到∠ABC=2∠DBC，∠ACB=2∠DCB，再根据三角形内角和定理得∠A+∠ABC+∠ACB=180°，∠BDC+∠DBC+∠DCB=180°，根据等式的性质变形得∠A=2∠BDC-180°，然后把∠BDC=120°代入计算即可．
∵BD、CD分别平分∠ABC和∠ACB，
∴∠ABC=2∠DBC，∠ACB=2∠DCB，
∵∠A+∠ABC+∠ACB=180°，∠BDC+∠DBC+∠DCB=180°，
∴∠A+2（∠DBC+∠DCB）=180°，
∴∠A+2（180°-∠BDC）=180°，
∴∠A=2∠BDC-180°，
而∠BDC=120°，
∴∠A=2×120°-180°=60°．
故选：C.
开心蛙口算题卡系列答案科目：初中数学 来源： 题型：
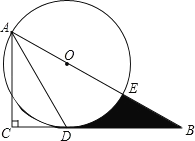
【题目】如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于D．以AB上某一点O为圆心作⊙O，使⊙O经过点A和点D．
（1）判断直线BC与⊙O的位置关系，并说明理由；
（2）若AC=3，∠B=30°．
①求⊙O的半径；
②设⊙O与AB边的另一个交点为E，求线段BD、BE与劣弧DE所围成的阴影部分的图形面积．（结果保留根号和π）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】沿河岸有
，
，
三个港口，甲、乙两船同时分别从，港口出发，匀速驶向港，最终到达港.设甲、乙两船行驶
后，与港的距离分别为
，
，，
与
的函数关系如图所示.则：
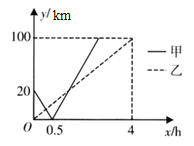
①从港到港全程为______
；
②如果两船相距小于
能够相互望见，那么在甲船到达港前甲、乙两船可以相互望见时，的取值范围是______.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】探究问题：已知
，画一个角
，使
，且
交
于点
.与有怎样的数量关系？
（1）我们发现与有两种位置关系：如图1与图2所示.
①图1中与数量关系为____________；图2中与数量关系为____________.请选择其中一种情况说明理由.
②由①得出一个真命题(用文字叙述):____________________________.
（2）应用②中的真命题，解决以下问题：若两个角的两边互相平行，且一个角比另一个角的2倍少30°，请直接写出这两个角的度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将一个边长为
的正方形图形分割成四部分(两个正方形和两个长方形)，请认真观察图形，解答下列问题:
(1)根据图中条件，请用两种方法表示该图形的总面积(用含
的代数式表示出来);
(2)如果图中的
满足
求的值;
(3)已知
,求
的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一艘海上巡逻船在A地巡航，这时接到B地海上指挥中心紧急通知：在指挥中心北偏西60°向的C地，有一艘渔船遇险，要求马上前去救援．此时C地位于北偏西30°方向上，A地位于B地北偏西75°方向上，A、B两地之间的距离为16海里．求A、C两地之间的距离．（保留根号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AC是⊙O的直径，BC是⊙O的弦，点P是⊙O外一点，连接PA，PB，AB，已知∠PBA=∠C．
（1）求证：PB是⊙O的切线；
（2）连接OP，若OP∥BC，且OP=8，⊙O的半径为
，求BC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】寒假即将到来，外出旅游的人数逐渐增多，对旅行包的需求也将增多，某店准备到生产厂家购买旅行包，该厂有甲、乙两种新型旅行包．若购进10个甲种旅行包和20个乙种旅行包共需5600元，若购进20个甲种旅行包和10个乙种旅行包共需5200元．
（1）甲、乙两种旅行包的进价分别是多少元？
（2）若该店恰好用了7000元购买旅行包；
①设该店购买了m个甲种旅行包，求该店购买乙种旅行包的个数；
②若该店将甲种旅行包的售价定为298元，乙种旅行包的售价定为325元，则当该店怎么样进货，才能获得最大利润，并求出最大利润．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
