
【题目】如图,在![]() 中,已知
中,已知![]() ,
,![]() 是
是![]() 边上一点,
边上一点,![]() ,
,![]() 平分
平分![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() .
.
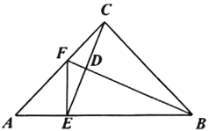
(1)若![]() ,求
,求![]() 和
和![]() 的度数;
的度数;
(2)若![]() ,求证
,求证![]() .
.
【答案】(1)70°;30°;(2)见解析
【解析】
(1)根据等边对等角求出∠CAB和∠CBA的度数,再根据等边对等角求出∠BEC和∠BCE的度数,从而可得出∠ACE的度数,最后根据外角的性质可求出∠BEC的度数;再证明△BCF≌△BEF,从而得出∠BEF的度数,最后得出∠FEC的度数.
(2)先根据(1)中全等得出EF=CF,再由等角对等边判定△AEF为等腰三角形,得出AE=EF,从而得出结果.
证明:(1)∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() 平分
平分![]() ,∴∠CBF=∠EBF,
,∴∠CBF=∠EBF,
在△BCF和△BEF中,
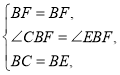
∴△BCF≌△BEF(SAS).
∴∠BEF=∠BCF=100°,.
∴∠FEC=∠BEF-∠BEC=30°.
(2)由(1)可知![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图△PAB中,PA=PB,C、D是直线AB上两点,连接PC、PD.
(1)请添加一个条件: ,使图中存在两个三角形全等.
(2)证明(1)的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC的度数为( )
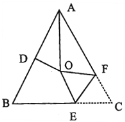
A.120°B.108°C.110°D.102°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取利了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:
根据所给信息,解答下列问题:
(1)在表中的频数分布表中,m= ,n= .
成绩 | 频数 | 频率 |
60≤x<70 | 60 | 0.30 |
70≤x<80 | m | 0.40 |
80≤x<90 | 40 | n |
90≤x≤100 | 20 | 0.10 |
(2)请补全图中的频数分布直方图.

(3)按规定,成绩在80分以上(包括80分)的选手进入决赛.若娄底市共有4000人参数,请估计约有多少人进入决赛?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,
(1)求证:△ACE≌△BCD;
(2)若DE=13,BD=12,求线段AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
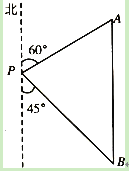
【题目】五一期间,小红到美丽的世界地质公园湖光岩参加社会实践活动,在景点P处测得景点B位于南偏东45°方向;然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与B之间的距离.(结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+3与坐标轴分别交于A,B两点,抛物线y=ax2+bx-3a经过点A,B,顶点为C,连接CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称.

(1)求抛物线的解析式及顶点C的坐标;
(2)求证:四边形ABCD是直角梯形.
【答案】(1)y=-x2-2x+3,顶点C的坐标为(-1,4);(2)证明见解析.
【解析】
(1)解:∵y=x+3与坐标轴分别交与A,B两点,∴A点坐标(-3,0)、B点坐标(0,3).
∵抛物线y=ax2+bx-3a经过A,B两点,
∴![]()
解得![]()
∴抛物线解析式为:y=-x2-2x+3.
∵y=-x2-2x+3=-(x+1)2+4,
∴顶点C的坐标为(-1,4).
(2)证明:∵B,D关于MN对称,C(-1,4),B(0,3),
∴D(-2,3).∵B(0,3),A(-3,0),∴OA=OB.
又∠AOB=90°,∴∠ABO=∠BAO=45°.
∵B,D关于MN对称,∴BD⊥MN.
又∵MN⊥x轴,∴BD∥x轴.
∴∠DBA=∠BAO=45°.
∴∠DBO=∠DBA+∠ABO=45°+45°=90°.
设直线BC的解析式为y=kx+b,
把B(0,3),C(-1,4)代入得,
![]() 解得
解得![]()
∴y=-x+3.
当y=0时,-x+3=0,x=3,∴E(3,0).
∴OB=OE,又∵∠BOE=90°,
∴∠OEB=∠OBE=∠BAO=45°.
∴∠ABE=180°-∠BAE-∠BEA=90°.
∴∠ABC=180°-∠ABE=90°.
∴∠CBD=∠ABC-∠ABD=45°.
∵CM⊥BD,∴∠MCB=45°.
∵B,D关于MN对称,
∴∠CDM=∠CBD=45°,CD∥AB.
又∵AD与BC不平行,∴四边形ABCD是梯形.
∵∠ABC=90°,∴四边形ABCD是直角梯形.
【题型】解答题
【结束】
21
【题目】有两组卡片,第一组三张卡片上都写着A、B、B,第二组五张卡片上都写着A、B、B、D、E.试用列表法求出从每组卡片中各抽取一张,两张都是B的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com