
【题目】如图△PAB中,PA=PB,C、D是直线AB上两点,连接PC、PD.
(1)请添加一个条件: ,使图中存在两个三角形全等.
(2)证明(1)的结论.

【答案】(1) AC=BD;(2)证明见解析.
【解析】
试题
本题所添条件不是唯一的,如,添上AC=BD(或PC=PD或∠PCA=∠PDB或∠CPB=∠DPA等),结合PA=PB都可证得△PBC≌△PAD或△PAC≌△PBD.
试题解析:
(1)本题答案不唯一,添上AC=BD(或PC=PD或∠PCA=∠PDB或∠CPB=∠DPA等),结合已知条件PA=PB可使图中存在两个全等三角形,如△PBC≌△PAD或△PAC≌△PBD.
(2)现选择添加条件:AC=BD,证△PAC≌△PBD,过程如下:
∵PA=PB,
∴∠PAB=∠PBA,
∴180°-∠PAB=180°-∠PBA,即∠PAC=∠PBD,
又∵AC=BD,
∴△PAC≌△PBD.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一动点,过点
上一动点,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,延长
,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,若
,若![]() ,设
,设![]() 长为
长为![]() ,
,![]() 长为
长为![]() ,则
,则![]() 关于
关于![]() 的函数关系式为__________.(不需写出
的函数关系式为__________.(不需写出![]() 的取值范围)
的取值范围)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() (x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB丄x轴于点B,点A与点B关于y轴对称.
(x>0)的图象交于点P(n,2),与x轴交于点A(-4,0),与y轴交于点C,PB丄x轴于点B,点A与点B关于y轴对称.

(1)求一次函数、反比例函数的解析式;
(2)求证:点C为线段AP的中点;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形,如果存在,说明理由并求出点D的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程,解应用题:
第二届中国国际进口博览会于2019年11月5日至10日在上海国家会展中心举行.与首届相比,第二届进博会的展览面积更大,企业展设置科技生活、汽车、装备等七个展区,展览面积由的270 000平方米增加到330 000平方米.参展企业比首届多了约300家,参展企业平均展览面积增加了12.8%,求首届进博会企业平均展览面积.
(1)在解应用题时,我们常借助表格、线段图等分析题目中的数量关系.
设首届进博会企业平均展览面积为x平方米,把下表补充完整:
届别 | 总面积(平方米) | 参展企业数量 | 企业平均展览面积(平方米) |
首 届 | 270 000 | x | |
第二届 | 330 000 |
(2)根据以上分析,列出方程(不解方程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
与x轴相交于A、B两点,其中A点的坐标为(-3,0)。

(1)求点B的坐标;
(2)已知![]() ,C为抛物线与y轴的交点。
,C为抛物线与y轴的交点。
①若点P在抛物线上,且![]() ,求点P的坐标;
,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC右侧作射线CP,∠ACP=![]() (0°<
(0°<![]() <60°),点A关于射线CP的对称点为点D,BD交CP于点E,连接AD,AE.
<60°),点A关于射线CP的对称点为点D,BD交CP于点E,连接AD,AE.

(1)求∠DBC的大小(用含![]() 的代数式表示);
的代数式表示);
(2)在![]() (0°<
(0°<![]() <60°)的变化过程中,∠AEB的大小是否发生变化?如果发生变化,请直接写出变化的范围;如果不发生变化,请直接写出∠AEB的大小;
<60°)的变化过程中,∠AEB的大小是否发生变化?如果发生变化,请直接写出变化的范围;如果不发生变化,请直接写出∠AEB的大小;
(3)用等式表示线段AE,BD,CE之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强语文课外阅读,某年级积极组织学生参加课外阅读读书分享会活动.从年级推荐的四种读物A:《水浒传》、B:《骆驼祥子》、C:《昆虫记》、D:《朝花夕拾》中选择一本读物每周一与班级同学分享读书体会。读书分享会活动组随机抽取本年级的部分学生,调查他们这四本读物中最喜爱一本读物,并将调查结果绘制成如下两幅不完整的统计图,请你结合图中的信息解答下列问题:

(1)求被调查的学生人数;
(2)补全条形统计图;
(3)已知该年级有![]() 名学生,估计全年级最喜爱《水浒传》的学生有多少人?
名学生,估计全年级最喜爱《水浒传》的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
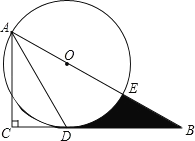
【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com