
【题目】如图,在等边三角形ABC右侧作射线CP,∠ACP=![]() (0°<
(0°<![]() <60°),点A关于射线CP的对称点为点D,BD交CP于点E,连接AD,AE.
<60°),点A关于射线CP的对称点为点D,BD交CP于点E,连接AD,AE.

(1)求∠DBC的大小(用含![]() 的代数式表示);
的代数式表示);
(2)在![]() (0°<
(0°<![]() <60°)的变化过程中,∠AEB的大小是否发生变化?如果发生变化,请直接写出变化的范围;如果不发生变化,请直接写出∠AEB的大小;
<60°)的变化过程中,∠AEB的大小是否发生变化?如果发生变化,请直接写出变化的范围;如果不发生变化,请直接写出∠AEB的大小;
(3)用等式表示线段AE,BD,CE之间的数量关系,并证明.
【答案】(1)∠DBC![]() ;(2)∠AEB的大小不会发生变化,且∠AEB=60°;(3)BD=2AE+CE,证明见解析.
;(2)∠AEB的大小不会发生变化,且∠AEB=60°;(3)BD=2AE+CE,证明见解析.
【解析】
(1)如图1,连接CD,由轴对称的性质可得AC=DC,∠DCP=∠ACP=![]() ,由△ABC是等边三角形可得AC=BC,∠ACB=60°,进一步即得∠BCD=
,由△ABC是等边三角形可得AC=BC,∠ACB=60°,进一步即得∠BCD=![]() ,BC=DC,然后利用三角形的内角和定理即可求出结果;
,BC=DC,然后利用三角形的内角和定理即可求出结果;
(2)设AC、BD相交于点H,如图2,由轴对称的性质可证明△ACE≌△DCE,可得∠CAE=∠CDE,进而得∠DBC=∠CAE,然后根据三角形的内角和可得∠AEB=∠BCA,即可作出判断;
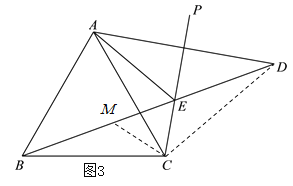
(3)如图3,在BD上取一点M,使得CM=CE,先利用三角形的外角性质得出∠BEC![]() ,进而得△CME是等边三角形,可得∠MCE=60°,ME=CE,然后利用角的和差关系可得∠BCM=∠DCE,再根据SAS证明△BCM≌△DCE,于是BM=DE,进一步即可得出线段AE,BD,CE之间的数量关系.
,进而得△CME是等边三角形,可得∠MCE=60°,ME=CE,然后利用角的和差关系可得∠BCM=∠DCE,再根据SAS证明△BCM≌△DCE,于是BM=DE,进一步即可得出线段AE,BD,CE之间的数量关系.
解:(1)如图1,连接CD,∵点A关于射线CP的对称点为点D,∴AC=DC,∠DCP=∠ACP=![]() ,
,
∵△ABC是等边三角形,∴AC=BC,∠ACB=60°,
∴∠BCD=![]() ,BC=DC,
,BC=DC,
∴∠DBC=∠BDC![]() ;
;

(2)∠AEB的大小不会发生变化,且∠AEB=60°.
理由:设AC、BD相交于点H,如图2,∵点A关于射线CP的对称点为点D,
∴AC=DC,AE=DE,又∵CE=CE,∴△ACE≌△DCE(SSS),∴∠CAE=∠CDE,
∵∠DBC=∠BDC,∴∠DBC=∠CAE,又∵∠BHC=∠AHE,∴∠AEB=∠BCA=60°,
即∠AEB的大小不会发生变化,且∠AEB=60°;

(3)AE,BD,CE之间的数量关系是:BD=2AE+CE.
证明:如图3,在BD上取一点M,使得CM=CE,
∵∠BEC=∠BDC+∠DCE=![]() ,
,
∴△CME是等边三角形,∴∠MCE=60°,ME=CE,
∴![]() ,
,
∴∠BCM=∠DCE,又∵BC=DC,CM=CE,
∴△BCM≌△DCE(SAS),∴BM=DE,
∵AE=DE,
∴BD=BM+ME+DE=2DE+ME=2AE+CE.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的布袋中装有4个只有颜色不同的球,其中1个黄球、1个蓝球、2个红球.
(1)任意摸出1个球,记下颜色后不放回,再任意摸出1个球.求两次摸出的球恰好都是红球的概率(要求画树状图或列表);
(2)现再将n个黄球放入布袋,搅匀后,使任意摸出1个球是黄球的概率为![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+1(a<0)的图象过点(1,0)和(x1,0),且﹣2<x1<1,下列5个判断中:①b<0;②b﹣a<0;③a>b﹣1;④a<﹣![]() ;⑤2a<b+
;⑤2a<b+![]() ,正确的是( )
,正确的是( )
A. ①③ B. ①②③ C. ①②③⑤ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年12月18日,新版《北京市生活垃圾管理条例》正式发布,并将在2020年5月1日起正式实施,这标志着北京市生活垃圾分类将正式步入法制化、常态化、系统化轨道.目前,相关配套设施的建设已经开启.如图,计划在某小区道路l上建一个智能垃圾分类投放点O,使得道路l附近的两栋住宅楼A,B到智能垃圾分类投放点O的距离相等.


(1)请在图中利用尺规作图(保留作图痕迹,不写作法),确定点O的位置;
(2)确定点O位置的依据为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△PAB中,PA=PB,C、D是直线AB上两点,连接PC、PD.
(1)请添加一个条件: ,使图中存在两个三角形全等.
(2)证明(1)的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是等边三角形,点
是等边三角形,点![]() 在射线
在射线![]() 上,延长
上,延长![]() 至
至![]() ,使
,使![]() .
.


(1)如图(1),当点![]() 为线段
为线段![]() 中点时,求证:
中点时,求证:![]() .
.
(2)如图(2),当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,![]() 还成立吗?若成立,请给予证明;若不成立,请说明理由.
还成立吗?若成立,请给予证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学习了勾股定理后,数学活动兴趣小组的小娟和小燕对离教室不远的一个直角三角形花台斜边上的高进行了探究:两人在直角边![]() 上距直角顶点
上距直角顶点![]() 米远的点
米远的点![]() 处同时开始测量,点
处同时开始测量,点![]() 为终点.小娟沿
为终点.小娟沿![]() 的路径测得所经过的路程是
的路径测得所经过的路程是![]() 米,小燕沿
米,小燕沿![]() 的路径测得所经过的路程也是
的路径测得所经过的路程也是![]() 米,这时小娟说我能求出这个直角三角形的花台斜边上的高了,小燕说我也知道怎么求出这个直角三角形的花台斜边上的高了.亲爱的同学们你能求出这个直角三角形的花台斜边上的高吗?若能,请你求出来:若不能,请说明理由?
米,这时小娟说我能求出这个直角三角形的花台斜边上的高了,小燕说我也知道怎么求出这个直角三角形的花台斜边上的高了.亲爱的同学们你能求出这个直角三角形的花台斜边上的高吗?若能,请你求出来:若不能,请说明理由?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大拇指与小指尽量张开时,两指尖的距离称为指距,某项研究表明,一般情况下人的身高h是指距d的一次函数,下表是测得指距与身高的一组数据:
(1)求出h与d之间的函数关系式;
(2)某人身高为196cm,一般情况下他的指距应是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,
(1)求证:△ACE≌△BCD;
(2)若DE=13,BD=12,求线段AB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com