练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，大拇指与小指尽量张开时，两指尖的距离称为指距，某项研究表明，一般情况下人的身高h是指距d的一次函数，下表是测得指距与身高的一组数据：

    （1）求出h与d之间的函数关系式；

    （2）某人身高为196cm,一般情况下他的指距应是多少？

    【答案】(1) h=9d20；(2) 24cm.

    【解析】

    （1）根据题意设h与d之间的函数关系式为：h=kd+b，利用待定系数法从表格中取两组数据，利用待定系数法，求得函数关系式；
    （2）把h=196代入函数解析式即可求得．

    (1)设h与d之间的函数关系式为：h=kd+b.

    把d=20,h=160;d=21,h=169,

    分别代入得,.

    解得k=9，b=20，

    即h=9d20；

    (2)当h=196时，196=9d20，

    解得d=24cm.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某天，某同学早上8点坐车从余姚图书馆出发去宁波大学，汽车离开余姚图书馆的距离（千米）与所用时间（分）之间的函数关系如图所示.已知汽车在途中停车加油一次，则下列描述不正确的是（ ）

    A.汽车在途中加油用了10分钟

    B.若，则加满油以后的速度为80千米/小时

    C.若汽车加油后的速度是90千米/小时，则

    D.该同学到达宁波大学

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在等边三角形ABC右侧作射线CP，∠ACP=（0°<<60°），点A关于射线CP的对称点为点D，BD交CP于点E，连接AD，AE.

    （1）求∠DBC的大小（用含的代数式表示）；

    （2）在（0°<<60°）的变化过程中，∠AEB的大小是否发生变化？如果发生变化，请直接写出变化的范围；如果不发生变化，请直接写出∠AEB的大小；

    （3）用等式表示线段AE，BD，CE之间的数量关系，并证明.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了创建全国卫生城市，某社区要清理一个卫生死角内的垃圾，租用甲、乙两车运送，两车各运12趟可完成，需支付运费4800元．已知甲、乙两车单独运完此堆垃圾，乙车所运趟数是甲车的2倍，且乙车每趟运费比甲车少200元．

    （1）求甲、乙两车单独运完此堆垃圾各需运多少趟？

    （2）若单独租用一台车，租用哪台车合算？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC边于D．以AB上某一点O为圆心作⊙O，使⊙O经过点A和点D．

    （1）判断直线BC与⊙O的位置关系，并说明理由；

    （2）若AC=3，∠B=30°．

    ①求⊙O的半径；

    ②设⊙O与AB边的另一个交点为E，求线段BD、BE与劣弧DE所围成的阴影部分的图形面积．（结果保留根号和π）

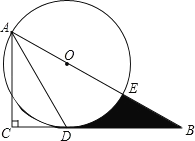
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了解某市市民晚饭后1小时内的生活方式，调查小组设计了“阅读”、“锻炼”、“看电视”和“其它”四个选项，用随机抽样的方法调查了该市部分市民，并根据调查结果绘制成如下统计图．

    根据统计图所提供的信息，解答下列问题：

    （1）本次共调查了 名市民；

    （2）补全条形统计图；

    （3）该市共有480万市民，估计该市市民晚饭后1小时内锻炼的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（本题12分）如图甲，在平面直角坐标系中，直线y=x+8分别交x轴、y轴于点A、B，⊙O的半径为2个单位长度．点P为直线y=x+8上的动点，过点P作⊙O的切线PC、PD，切点分别为C、D，且PC⊥PD．

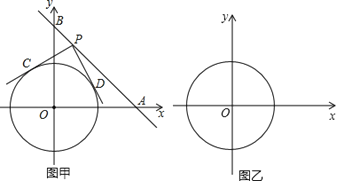
    （1）试说明四边形OCPD的形状（要有证明过程）；

    （2）求点P的坐标；

    （3）如图乙，若直线y=x+b将⊙O的圆周分成两段弧长之比为1：3，请直接写出b的值

    （4）向右移动⊙O（圆心O始终保持在x轴上），试求出当⊙O与直线y=x+8有交点时圆心O的横坐标m的取值范围。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，BC＝2AB＝4，点E，F分别是BC，AD的中点．

    (1)求证：△ABE≌△CDF；

    (2)当四边形AECF为菱形时，求出该菱形的面积．

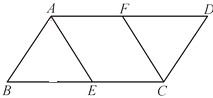
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将一个边长为的正方形图形分割成四部分(两个正方形和两个长方形)，请认真观察图形，解答下列问题:

    (1)根据图中条件，请用两种方法表示该图形的总面积(用含的代数式表示出来);

    (2)如果图中的满足求的值;

    (3)已知,求的值.

    查看答案和解析>>

    同步练习册答案