
【题目】已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
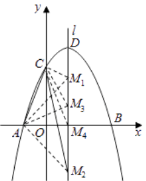
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
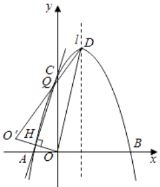
(4)问:若抛物线顶点为D,点Q为直线AC上一动点,当△DOQ的周长最小时,求点Q的坐标
【答案】
(1)
解:方法一:
将A(﹣1,0)、B(3,0)、C(0,3)代入抛物线y=ax2+bx+c中,得:
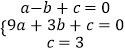 ,
,
解得: 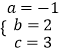
∴抛物线的解析式:y=﹣x2+2x+3
方法二:
∵A(﹣1,0)、B(3,0)、C(0,3),
∴y=﹣(x+1)(x﹣3),即y=﹣x2+2x+3
(2)
解:方法一:
连接BC,直线BC与直线l的交点为P;
∵点A、B关于直线l对称,
∴PA=PB,
∴BC=PC+PB=PC+PA
设直线BC的解析式为y=kx+b(k≠0),将B(3,0),C(0,3)代入上式,得:
![]() ,解得:
,解得: ![]()
∴直线BC的函数关系式y=﹣x+3;
当x=1时,y=2,即P的坐标(1,2)
方法二:
连接BC,
∵l为对称轴,
∴PB=PA,
∴C,B,P三点共线时,△PAC周长最小,把x=1代入lBC:y=﹣x+3,得P(1,2)

(3)
解:方法一:
抛物线的对称轴为:x=﹣ ![]() =1,设M(1,m),已知A(﹣1,0)、C(0,3),则:
=1,设M(1,m),已知A(﹣1,0)、C(0,3),则:
MA2=m2+4,MC2=(3﹣m)2+1=m2﹣6m+10,AC2=10;
①若MA=MC,则MA2=MC2,得:
m2+4=m2﹣6m+10,得:m=1;
②若MA=AC,则MA2=AC2,得:
m2+4=10,得:m=± ![]() ;
;
③若MC=AC,则MC2=AC2,得:
m2﹣6m+10=10,得:m1=0,m2=6;
当m=6时,M、A、C三点共线,构不成三角形,不合题意,故舍去;
综上可知,符合条件的M点,且坐标为 M(1, ![]() )(1,﹣
)(1,﹣ ![]() )(1,1)(1,0).
)(1,1)(1,0).
方法二:
设M(1,t),A(﹣1,0),C(0,3),
∵△MAC为等腰三角形,
∴MA=MC,MA=AC,MC=AC,
(1+1)2+(t﹣0)2=(1﹣0)2+(t﹣3)2,∴t=1,
(1+1)2+(t﹣0)2=(﹣1﹣0)2+(0﹣3)2,∴t=± ![]() ,
,
(1﹣0)2+(t﹣3)2=(﹣1﹣0)2+(0﹣3)2,∴t1=6,t2=0,
经检验,t=6时,M、A、C三点共线,故舍去,
综上可知,符合条件的点有4个,M1(1, ![]() ),M2(1,﹣
),M2(1,﹣ ![]() ),M3(1,1),M4(1,0)
),M3(1,1),M4(1,0)
(4)
解:作点O关于直线AC的对称点O交AC于H,
作HG⊥AO,垂足为G,
∴∠AHG+∠GHO=90°,∠AHG+∠GAH=90°,
∴∠GHO=∠GAH,
∴△GHO∽△GAH,
∴HG2=GOGA,
∵A(﹣1,0),C(0,3),
∴lAC:y=3x+3,H(﹣ ![]() ,
, ![]() ),
),
∵H为OO′的中点,
∴O′(﹣ ![]() ,
, ![]() ),
),
∵D(1,4),
∴lO′D:y= ![]() x+
x+ ![]() ,lAC:y=3x+3,
,lAC:y=3x+3,
∴x=﹣ ![]() ,y=
,y= ![]() ,
,
∴Q(﹣ ![]() ,
, ![]() )
)
【解析】方法一:(1)直接将A、B、C三点坐标代入抛物线的解析式中求出待定系数即可.(2)由图知:A、B点关于抛物线的对称轴对称,那么根据抛物线的对称性以及两点之间线段最短可知:若连接BC,那么BC与直线l的交点即为符合条件的P点.(3)由于△MAC的腰和底没有明确,因此要分三种情况来讨论:①MA=AC、②MA=MC、③AC=MC;可先设出M点的坐标,然后用M点纵坐标表示△MAC的三边长,再按上面的三种情况列式求解.
方法二:(1)略.(2)找出A点的对称点点B,根据C,P,B三点共线求出BC与对称轴的交点P.(3)用参数表示的点M坐标,分类讨论三种情况,利用两点间距离公式就可求解.(4)先求出AC的直线方程,利用斜率垂直公式求出OO’斜率及其直线方程,并求出H点坐标,进而求出O’坐标,求出DO’直线方程后再与AC的直线方程联立,求出Q点坐标.
【考点精析】根据题目的已知条件,利用二次函数的概念的相关知识可以得到问题的答案,需要掌握一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数.


科目:初中数学 来源: 题型:
【题目】为弘扬“敬老爱老”传统美德,某校八年级(1)班的学生要去距离学校10km的敬老院看望老人,一部分学生骑自行车先走,过了20min后,其余学生乘汽车出发,结果乘汽车的同学早到10min.已知汽车的速度是骑车学生的4倍,求骑车学生的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某化妆品店老板到厂家选购A、B两种品牌的化妆品,若购进A品牌的化妆品5套,B品牌的化妆品6套,需要950元;若购进A品牌的化妆品3套,B品牌的化妆品2套,需要450元.
![]() 求A、B两种品牌的化妆品每套进价分别为多少元?
求A、B两种品牌的化妆品每套进价分别为多少元?
![]() 若销售1套A品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套,且B品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货?
若销售1套A品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套,且B品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是 ( )
①2∠DCF=∠BCD; ②EF=CF; ③S△BEC=2S△CEF; ④∠DFE=3∠AEF.

A. ①②③④ B. ①②④ C. ①② D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了绿化环境,计划分两次购进A、B两种花草,第一次分别购进A、B两种花草30棵和15棵,共花费675元;第二次分别购进A、B两种花草12棵和5棵.两次共花费940元(两次购进的A、B两种花草价格均分别相同).
(1)A、B两种花草每棵的价格分别是多少元?
(2)若购买A、B两种花草共31棵,且B种花草的数量少于A种花草的数量的2倍,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校对学生的课外阅读时间进行抽样调查,将收集的数据分成A、B、C、D、E五组进行整理,并绘制成如下的统计图表(图中信息不完整).
组别 | 阅读时间x(时) | 人数 |
A | 0≤x<10 | k |
B | 10≤x<20 | 100 |
C | 20≤x<30 | m |
D | 30≤x<40 | 140 |
E | x≥40 | n |

请结合以上信息解答下列问题
(1)阅读时间分组统计表中k、m、n的值分别是 、 、 ;
(2)补全“阅读人数分组统计图”;
(3)若全校有3000名学生,请估算全校课外阅读时间在20小时以下(不含20小时)的
查看答案和解析>>
科目:初中数学 来源: 题型:
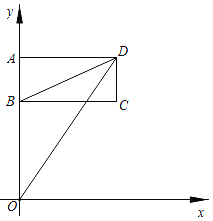
【题目】如图,长方形ABCD在平面直角坐标系中,已知点A(0,a),B(0,6),C(b,6),且满足a=![]() +8.
+8.
(1)请直接写出A、C、D三个点的坐标,A ,C ,D ;
(2)连接线段BD、OD,试求三角形BOD的面积;
(3)若长方形ABCD以每秒1个单位长度匀速向下运动,设运动的时间为t秒,问是否存在某一时刻,三角形BOD的面积与长方形ABCD的面积相等?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑公司开发出一种软件,从研发到年初上市后,经历了从亏损到盈利的过程,如图中的图象是抛物线的一段,它刻画了该软件上市以来累积利润S(万元)与销售时间t(月)之间的函数关系(即前t个月的利润总和S与t之间的函数关系),根据图象提供的信息,解答下列问题: 
(1)该种软件上市第几个月后开始盈利?
(2)求累积利润S(万元)与时间t(月)之间的函数表达式;
(3)截止到几月末,公司累积利润达到30万元?
(4)求公司第6个月末所累积的利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE. 
(1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若AF=6,EF=2 ![]() ,求⊙O 的半径长.
,求⊙O 的半径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com