
【题目】如图,已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 与直线交于
与直线交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 、
、![]() 两点,且
两点,且![]() 点坐标为(1,0).
点坐标为(1,0).
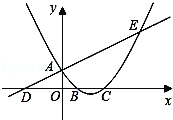
(1)求该抛物线的解析式;
(2)动点![]() 在
在![]() 轴上移动,当△
轴上移动,当△![]() 是直角三角形时,直接写出点
是直角三角形时,直接写出点![]() 的坐标;
的坐标;
(3)在抛物线的对称轴上找一点![]() ,使|
,使|![]() |的值最大,求出点
|的值最大,求出点![]() 的坐标.
的坐标.
【答案】(1)、y=![]() x2﹣
x2﹣![]() x+1;(2)、(
x+1;(2)、(![]() ,0)或(1,0)或(3,0)或(
,0)或(1,0)或(3,0)或(![]() ,0);(3)、M(1.5,-0.5)
,0);(3)、M(1.5,-0.5)
【解析】试题分析:(1)首先根据直线解析式求出点A、B的坐标,然后代入二次函数解析式得出解析式;(2)根据直角三角形的性质得出点P的坐标;(3)首先得出抛物线的对称轴,则MC=MB,要使|AM﹣MC|最大,即是使|AM﹣MB|最大,由三角形两边之差小于第三边得,当A、B、M在同一直线上时|AM﹣MB|的值最大,求出直线AB的解析式,直线AB与对称轴的交点就是点M.
试题解析:(1)直线![]() 与
与![]() 轴交于点
轴交于点![]() 得A(0,1),
得A(0,1),
将A(0,1)、B(1,0)坐标代入y=![]() x2+bx+c
x2+bx+c
得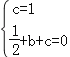 ,
,
解得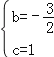 ,
,
∴抛物线的解折式为y=![]() x2﹣
x2﹣![]() x+1;
x+1;
(2)满足条件的点P的坐标为(![]() ,0)或(1,0)或(3,0)或(
,0)或(1,0)或(3,0)或(![]() ,0)
,0)
(3)抛物线的对称轴为![]()
∵B、C关于x=![]() 对称,
对称,
∴MC=MB,
要使|AM﹣MC|最大,即是使|AM﹣MB|最大,
由三角形两边之差小于第三边得,当A、B、M在同一直线上时|AM﹣MB|的值最大.
易知直线AB的解折式为y=﹣x+1
∴由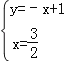 ,得
,得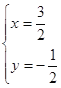
∴M(1.5,-0.5)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中A(-2,3),B(-3,1),C(-1,2)
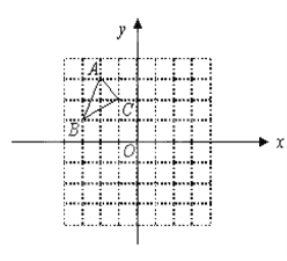
(1)画出△ABC关于![]() 轴、y轴对称的△A1B1C1和△A2B2C2;
轴、y轴对称的△A1B1C1和△A2B2C2;
(2)将△ABC绕原点O旋转1800,画出旋转后的△A3B3C3;
(3)在△A1B1C1,△A2B2C2,△A3B3C3中, 与 成轴对称,对称轴是 ;(填一组即可) 与 成中心对称,对称中心的坐标是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
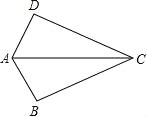
A.CB=CD B.∠BAC=∠DAC C.∠BCA=∠DCA D.∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果销售点用1000元购进甲、乙两种新出产的水果共140千克,这两种水果的进价、售价如表所示:
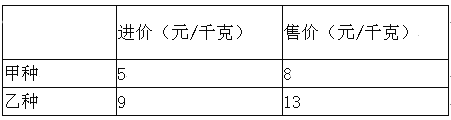
(1)这两种水果各购进多少千克?
(2)若该水果店按售价销售完这批水果,获得的利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com