
【题目】如图,△ABC中A(-2,3),B(-3,1),C(-1,2)
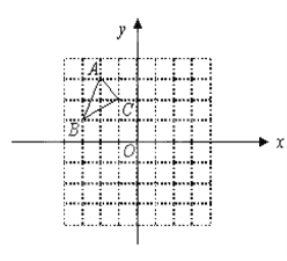
(1)画出△ABC关于![]() 轴、y轴对称的△A1B1C1和△A2B2C2;
轴、y轴对称的△A1B1C1和△A2B2C2;
(2)将△ABC绕原点O旋转1800,画出旋转后的△A3B3C3;
(3)在△A1B1C1,△A2B2C2,△A3B3C3中, 与 成轴对称,对称轴是 ;(填一组即可) 与 成中心对称,对称中心的坐标是
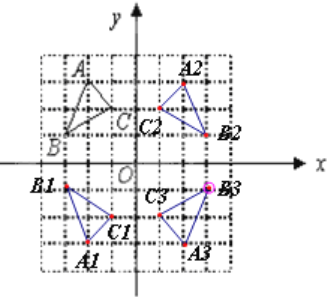
【答案】(1)见解析(2)见解析(3) △A1B1C1和△A3B3C3关于y轴对称或△A2B2C2和△A3B3C3,关于x轴对称;△A1B1C1和△A2B2C2关于原点成中心对称.
【解析】
试题分析:(1)分别确定点A、B、C关于![]() 轴、y轴的对称点A1、B1、C1和点A2、B2、C2;然后顺次连接各点即可;(2)分别确定点A、B、C关于原点的对称点A3、B3、C3,然后顺次连接各点即可;(3)观察图形即可得出结论.
轴、y轴的对称点A1、B1、C1和点A2、B2、C2;然后顺次连接各点即可;(2)分别确定点A、B、C关于原点的对称点A3、B3、C3,然后顺次连接各点即可;(3)观察图形即可得出结论.
试题解析:(1)如图:(2)如图:(3)△A1B1C1和△A3B3C3关于y轴对称或△A2B2C2和△A3B3C3,关于x轴对称;△A1B1C1和△A2B2C2关于原点成中心对称.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
【题目】一个两位数的个位数字是a,十位数字是b(b≠0),用代数式表示这个两位数为( )
A. 10b+a B. 10a+b C. b+a D. 100a+10b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为执行“均衡教育”政策,某县2014年投入教育经费2500万元,预计到2016年底三年累计投入1.2亿元.若每年投入教育经费的年平均增长 百分率为x,则下列方程正确的是( )
A.2500(1+x)2=1.2
B.2500(1+x)2=12000
C.2500+2500(1+x)+2500(1+x)2=1.2
D.2500+2500(1+x)+2500(1+x)2=12000
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列一段文字,在回答后面的问题.
已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离公式![]() ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)已知A(2,4)、B(﹣3,﹣8),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A、B两点间的距离.
(3)已知一个三角形各顶点坐标为A(0,6)、B(﹣3,2)、C(3,2),你能判定此三角形的形状吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的顶点坐标分别为 A(1,1),B(1,-1),C(-1,-1),D(-1,1),y轴上有一点 P(0,2).作点P关于点A的对称点P1,作点P1关于点B的对称点P2,作点P2关于点C的对称轴P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5,作点P5关于点B的对称点P6,…,按此操作下去,则点P2016的坐标为( )
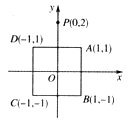
A. (0,2) B. (2,0) C. (0,-2) D. (-2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
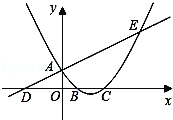
【题目】如图,已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 与直线交于
与直线交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 、
、![]() 两点,且
两点,且![]() 点坐标为(1,0).
点坐标为(1,0).
(1)求该抛物线的解析式;
(2)动点![]() 在
在![]() 轴上移动,当△
轴上移动,当△![]() 是直角三角形时,直接写出点
是直角三角形时,直接写出点![]() 的坐标;
的坐标;
(3)在抛物线的对称轴上找一点![]() ,使|
,使|![]() |的值最大,求出点
|的值最大,求出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com