
 如图,已知AC垂直平分BD,∠ABC=∠DAF,DF⊥BD
如图,已知AC垂直平分BD,∠ABC=∠DAF,DF⊥BD分析 (1)根据全等三角形的判定和性质、平行线的性质得出AF∥CD,进而利用平行四边形的判定解答即可;
(2)根据平行四边形和菱形的性质分析,再根据勾股定理解答即可.
解答 (1)证明:∵AC垂直平分BD,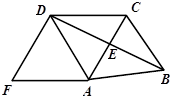
∴AB=AD,BC=DC,
又∵AC=AC,
在△ABC与△ADC中,
$\left\{\begin{array}{l}{AB=AD}\\{BC=DC}\\{AC=AC}\end{array}\right.$,
∴△ABC≌△ADC(SSS),
∴∠ABC=∠ADC,
∵∠ABC=∠DAF,
∴∠ADC=∠DAF,
∴AF∥CD,
∵AC⊥BD,DF⊥BD,
∴DF∥AC,
∴四边形ACDF是平行四边形;
(2)解:∵四边形ACDF是平行四边形,AF=DF=5,
∴?ACDF是菱形,
∴CD=AC=5,
∵AD=6,设CE=x,则AE=5-x,
∴CD2-CE2=AD2-AE2
即52-x2=62-(5-x)2
解得:x=$\frac{7}{5}$,即CE=$\frac{7}{5}$,
∴DE=$\sqrt{C{D}^{2}-C{E}^{2}}=\frac{24}{5}$,
∴BD=2DE=$\frac{48}{5}$.
点评 此题考查平行四边形的判定和性质,关键是根据全等三角形的判定和平行四边形的判定分析.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,连接AM、CN、MN.若AB=3$\sqrt{2}$,BC=2$\sqrt{3}$,则图中阴影部分的面积为3$\sqrt{6}$.
如图,矩形ABCD中,点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,连接AM、CN、MN.若AB=3$\sqrt{2}$,BC=2$\sqrt{3}$,则图中阴影部分的面积为3$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD∥BC,∠BAD=∠BCD.
如图,在四边形ABCD中,AD∥BC,∠BAD=∠BCD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -5a>-5b | B. | a-3>b-3 | C. | 4-a>4-b | D. | $\frac{1}{2}$a<$\frac{1}{2}$b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
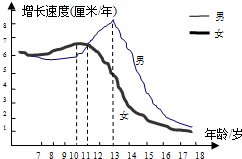 生物学研究表明,在8--17岁期间,男女生身高增长速度规律呈现如下图所示,请你观察此图,回答下列问题,男生身高增长速度的巅峰是几岁?在几岁时男生、女生的身高增长速度是一样的?
生物学研究表明,在8--17岁期间,男女生身高增长速度规律呈现如下图所示,请你观察此图,回答下列问题,男生身高增长速度的巅峰是几岁?在几岁时男生、女生的身高增长速度是一样的?查看答案和解析>>
科目:初中数学 来源:2016-2017学年福建省泉州市泉港区2016-2017学年八年级3月教学质量检测数学试卷(解析版) 题型:单选题
根据分式的基本性质,分式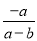 可变形为( )
可变形为( )
A. 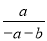 B.
B. 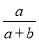 C.
C. 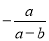 D.
D. 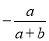
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com