
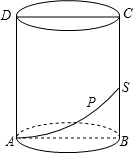
 如图,在圆柱的截面ABCD中,AB=$\frac{16}{π}$,BC=12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离为10.
如图,在圆柱的截面ABCD中,AB=$\frac{16}{π}$,BC=12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离为10. 科目:初中数学 来源: 题型:解答题
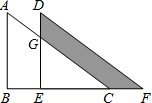 如图是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到三角形DEF,若AB=8cm,BE=4cm,DG=3cm,则图中阴影部分的面积是多少cm2?
如图是重叠的两个直角三角形,将其中一个直角三角形沿BC方向平移得到三角形DEF,若AB=8cm,BE=4cm,DG=3cm,则图中阴影部分的面积是多少cm2?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
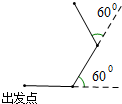 如图,小华在空旷的操场上向右行走20米后,接着向左转60°,再向前行走20米,再接着向左转,再向前行走20米,…这样一直走下去.
如图,小华在空旷的操场上向右行走20米后,接着向左转60°,再向前行走20米,再接着向左转,再向前行走20米,…这样一直走下去.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com