
(12分)如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
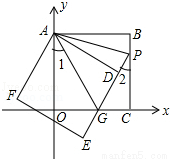
(1)求证:△AOG≌△ADG;
(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由.
(1)证明见试题解析;(2)PG=OG+BP,理由见试题解析.
【解析】
试题分析:(1)由AO=AD,AG=AG,利用“HL”可证△AOG≌△ADG;
(2)利用(1)的方法,同理可证△ADP≌△ABP,得出∠1=∠DAG,∠DAP=∠BAP,而∠1+∠DAG+∠DAP+∠BAP=90°,由此可求∠PAG的度数;根据两对全等三角形的性质,可得出线段OG、PG、BP之间的数量关系;
(3)由△AOG≌△ADG可知,∠AGO=∠AGD,而∠1+∠AGO=90°,∠2+∠PGC=90°,当∠1=∠2时,可证∠AGO=∠AGD=∠PGC,而∠AGO+∠AGD+∠PGC=180°,得出∠AGO=∠AGD=∠PGC=60°,即∠1=∠2=30°,解直角三角形求OG,PC,确定P、G两点坐标,得出直线PE的解析式.
试题解析:(1)∵∠AOG=∠ADG=90°,
在Rt△AOG和Rt△ADG中,∵AO=AD,AG-AG,∴△AOG≌△ADG(HL);
(2)PG=OG+BP.理由如下:
由(1)同理可证△ADP≌△ABP,则∠DAP=∠BAP,由(1)可知,∠1=∠DAG,又∠1+∠DAG+∠DAP+∠BAP=90°,∴2∠DAG+2∠DAP=90°,即∠DAG+∠DAP=45°,∴∠PAG=∠DAG+∠DAP=45°,
∵△AOG≌△ADG,△ADP≌△ABP,∴DG=OG,DP=BP,∴PG=DG+DP=OG+BP.
考点:全等三角形的判定与性质.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期第二次月度联考数学试卷(解析版) 题型:填空题
在△ABC中,AB=6,AC=9,点D在边AB所在的直线上,且AD=2,过点D作DE∥BC交边AC所在直线于点E,则CE的长为
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期第四次月考数学试卷(解析版) 题型:选择题
体育课上,九年级2名学生各练习10次立定跳远,要判断哪一名学生的成绩比较稳定,通常需要比较这两名学生立定跳远成绩的( )
A.平均数 B.众数 C .中位数 D.方差
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省龙岩市九年级上学期半期考试数学试卷(解析版) 题型:选择题
三角形两边长分别是8和6,第三边长是一元二次方程x2-16x+60=0一个实数根,则该三角形的面积是( )
A.24 B.48 C.24或8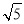 D.8
D.8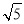
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省龙岩市九年级上学期半期考试数学试卷(解析版) 题型:选择题
直线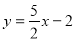 与抛物线
与抛物线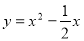 的交点个数是( )
的交点个数是( )
A.0个 B.1个 C.2个 D.互相重合的两个
查看答案和解析>>
科目:初中数学 来源:2013-2014学年湖北省咸宁市九年级上学期第二次月考数学试卷(解析版) 题型:填空题
如图,以正方形ABCD边BC为直径作半圆O,过点D作直线切半圆于点F,交AB于点E,则△ADE和直角梯形EBCD的周长之比为 .
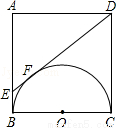
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com