
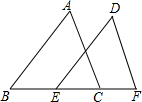
 如图,已知:∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,若要以“SAS”为依据,还缺条件AB=DE;若要以“ASA”为依据,还缺条件∠ACB=∠DFE,若要以“AAS”为依据,还缺条件∠A=∠D.
如图,已知:∠B=∠DEF,BC=EF,现要证明△ABC≌△DEF,若要以“SAS”为依据,还缺条件AB=DE;若要以“ASA”为依据,还缺条件∠ACB=∠DFE,若要以“AAS”为依据,还缺条件∠A=∠D. 分析 由于已知一组对应角相等,一组对应边相等,若利用SAS证全等,那么所需的另一边应该是已知角的夹边相等;若利用ASA证全等,则所需的另一角是以已知边为边的另一个角相等;若利用AAS证全等,所需的另一角是已知边的对角相等.
解答 解:已知:∠B=∠DEF,BC=EF.
若要以“SAS”为依据,还缺条件AB=DE;
若要以“ASA”为依据,还缺条件∠ACB=∠DFE;
若要以“AAS”为依据,还缺条件∠A=∠D.
故答案为AB=DE,∠ACB=∠DFE,∠A=∠D.
点评 此题主要考查了全等三角形的判定,关键是掌握判定两个三角形全等的一般方法:SSS、SAS、ASA、AAS、HL.三角形全等的判定是中考的热点,一般以考查三角形全等的方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.


科目:初中数学 来源: 题型:解答题
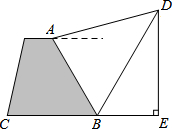 如图,小明站在看台上的A处,测得旗杆顶端D的仰角为15°,当旗杆顶端D的影子刚好落在看台底部B处时,太阳光与地面成60°角.已知∠ABC=60°,AB=4米,求旗杆的高度.(点A与旗杆DE及其影子在同一平面内,C、B、E三点共线且旗杆与地面垂直,不考虑小明的身高)
如图,小明站在看台上的A处,测得旗杆顶端D的仰角为15°,当旗杆顶端D的影子刚好落在看台底部B处时,太阳光与地面成60°角.已知∠ABC=60°,AB=4米,求旗杆的高度.(点A与旗杆DE及其影子在同一平面内,C、B、E三点共线且旗杆与地面垂直,不考虑小明的身高)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$=3$\sqrt{2}$ | B. | $\sqrt{{3}^{2}+{4}^{2}}$=3+4=7 | C. | (3$\sqrt{2}$)2=6 | D. | $\sqrt{3}$•$\sqrt{6}$=3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com