
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
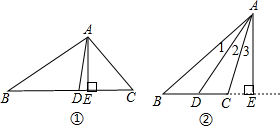 求证:三角形一个角的平分线与这个角的对边上的高所形成的夹角等于另两个角之差的一半.
求证:三角形一个角的平分线与这个角的对边上的高所形成的夹角等于另两个角之差的一半.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
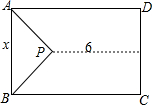 如图,一块矩形空地ABCD,除留下一块等腰直角△APB的空地外,其他都种植草皮.设AB=x米,直角顶点P到CD的距离为6米,草地的面积为y米2,求y与x之间的函数关系式.
如图,一块矩形空地ABCD,除留下一块等腰直角△APB的空地外,其他都种植草皮.设AB=x米,直角顶点P到CD的距离为6米,草地的面积为y米2,求y与x之间的函数关系式.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com