
【题目】一个直角三角形的两条直角边分别长3cm,4cm,则它的内心和外心之间的距离为________
【答案】![]()
【解析】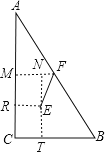
如图,E为直角三角形ABC的内心,F为直角三角形ABC的外心,
过E作ET⊥BC于T,ER⊥AC于R,过F作FM⊥AC于M,TE交FM于N,
则ER=ET,∠C=∠ERC=∠ETC=90°
∴ERCT是正方形,
∴ER=RC=CT=ET,
∵∠FMC=∠C=∠NTC=90°
∴四边形MCTN是矩形,
∴CT=MN,CM=NT,
∵F为AB中点,FM∥BC,
∴M为AC中点,
∴FM=![]() BC=1.5,MC=AM=2,
BC=1.5,MC=AM=2,
设直角三角形ABC的内切圆的半径是r,
则ER=RC=CT=ET,
根据切线长定理得:3r+4r=5,
r=1,
即ER=RC=CT=ET=MN=1,
∴MR=21=1,
在Rt△ENF中,EN=MR=1,FN=1.51=0.5,由勾股定理得:EF=![]() =
=![]() ,
,
故答案为:![]() .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知在数轴上有A、B两点,点A表示的数是![]() ,点B表示的数是9.点
,点B表示的数是9.点
P在数轴上从点A出发,以每秒2个单位的速度沿数轴正方向运动,同时,点Q在数轴上从
点B出发,以每秒3个单位的速度在沿数轴负方向运动,当点Q到达点A时,两点同时停止
运动.设运动时间为![]() 秒.
秒.
(1)AB= ; ![]() 时,点Q表示的数是 ;当
时,点Q表示的数是 ;当![]() 时,P、Q两点相遇;
时,P、Q两点相遇;
(2)如图2,若点M为线段AP的中点,点N为线段BP中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长;
(3)如图3,若点M为线段AP的中点,点T为线段BQ中点,则点M表示的数为________;点T表示的数为________ ;MT=_________ .(用含t的代数式填空)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,经过点A(-4,4)的抛物线y=ax2+bx+c与x轴相交于点B(-3,0)及原点O.
(1)求抛物线的解析式;
(2)如图1,过点A作AH⊥x轴,垂足为H,平行于y轴的直线交线段AO于点Q,交抛物线于点P,当四边形AHPQ为平行四边形时,求∠AOP的度数;
(3)如图2,若点C在抛物线上,且∠CAO=∠BAO,试探究:在(2)的条件下,是否存在点G,使得△GOP∽△COA?若存在,请求出所有满足条件的点G坐标;若不存在,请说明理由.
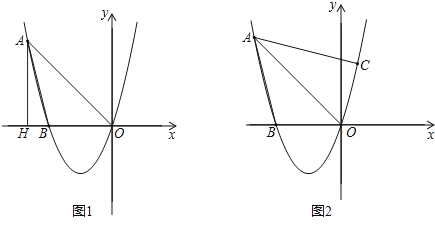
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(y+3)(y-2)=y2+my+n,则m、n的值分别为( )
A. m=5,n=6 B. m=1,n=-6 C. m=1,n=6 D. m=5,n=-6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列两个变量成反比例函数关系的是( )
①三角形底边为定值,它的面积S和这条边上的高线h;
②三角形的面积为定值,它的底边a与这条边上的高线h;
③面积为定值的矩形的长与宽;
④圆的周长与它的半径.
A.①④B.①③C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题.
例:若代数式![]() 的值是常数2,则a的取值范围 2≤a≤4 .
的值是常数2,则a的取值范围 2≤a≤4 .
分析:原式=|a﹣2|+|a﹣4|,而|a|表示数x在数轴上的点到原点的距离,|a﹣2|表示数a在数轴上的点到数2的点的距离,所以我们可以借助数轴进行分析.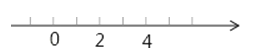
解:原式=|a﹣2|+|a﹣4|
在数轴上看,讨论a在数2表示的点左边;在数2表示的点和数4表示的点之间还是在数4表示的点右边,分析可得a的范围应是2≤a≤4.
(1)此例题的解答过程了用了哪些数学思想?请列举.
(2)化简![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com