
【题目】已知,m,n是一元二次方程x2+4x+3=0的两个实数根,且|m|<|n|,抛物线y=x2+bx+c的图象经过点A(m,0),B(0,n),如图所示.
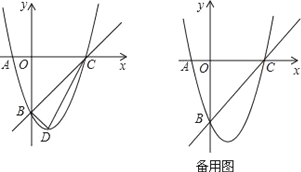
(1)求这个抛物线的解析式;
(2)若点D是直线BC下方抛物线上的动点,求△BCD面积最大时,点D的坐标及最大面积分别是多少?
【答案】(1)![]() ;(2)D
;(2)D![]() ,最大面积为
,最大面积为![]() .
.
【解析】
(1)先解一元二次方程,然后用待定系数法求出抛物线解析式;
(2)先求出点C坐标,然后设D点为(x,y),过点D作DE⊥y轴,垂足为E,过点C作CF⊥DE,交DE于点F,利用间接法求△BCD的面积,得到面积与x的二次函数,然后利用二次函数的性质,化为顶点式,即可得到点D的坐标和面积的最大值.
解(1)∵x2+4x+3=0,
∴x1=-1,x2=-3,
∵m,n是一元二次方程x2+4x+3=0的两个实数根,且|m|<|n|,
∴m=-1,n=-3,
∵抛物线y=x2+bx+c的图象经过点A(m,0),B(0,n),
∴![]() ,解得:
,解得:![]() ,
,
∴抛物线解析式为:![]() ;
;
(2)∵![]() ,
,
令![]() ,则
,则![]() ,
,
解得:![]() 或
或![]() ,
,
∴点C坐标为:(3,0),
∵点B为(0,-3),
设D点坐标为:(x,y),点D在第四象限,
如图:过点D作DE⊥y轴,垂足为E,过点C作CF⊥DE,交DE于点F,
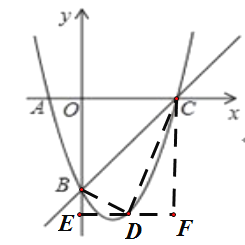
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
整理,得:![]() ,
,
∵![]() ,且
,且![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
∵![]() ,
,
∴当![]() 时,△BCD的面积取到最大值,
时,△BCD的面积取到最大值,
最大面积为:![]() ;
;
∴![]() ,
,
∴点D的坐标为:![]() ;
;
∴点D的坐标为:![]() ;△BCD的最大面积为
;△BCD的最大面积为![]() .
.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】已知⊙O半径为1,若点P在⊙O外且⊙O上存在点A、B使得∠APB=60°,则称点P是⊙O的领域点.
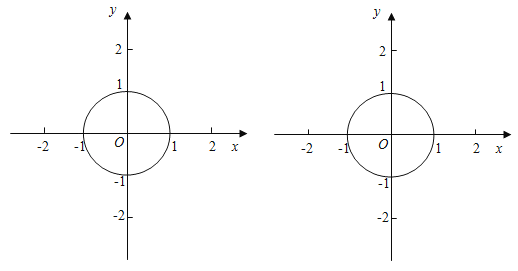
(1)对以下情况,用三角板或量角器尝试画图,并判断点P是否是⊙O的领域点(在横线上填“是”或“不是”).
①当OP=1.2时, 点P ⊙O的领域点
| ②当OP=2时, 点P ⊙O的领域点
| ③当OP=3时, 点P ⊙O的领域点
|
(2)若点P是⊙O的领域点,则OP的取值范围是 ;
(3)如图,以圆心O为坐标原点建立平面直角坐标系xOy,设直线y=﹣x+b(b>0)与x轴、y轴分别相交于点M、N.
①若线段MN上有且只有一个点是⊙O的领域点,求b的值;
②若线段MN上存在⊙O的领域点,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是正
是正![]() 内一点,
内一点,![]() ,
,![]() ,
,![]() ,将线段
,将线段![]() 以点
以点![]() 为旋转中心逆时针旋转
为旋转中心逆时针旋转![]() 得到线段
得到线段![]() ,下列结论:①
,下列结论:①![]() 可以由
可以由![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到;②点
得到;②点![]() 与
与![]() 的距离为6;③
的距离为6;③![]() ;④
;④![]() ;⑤
;⑤![]() . 其中正确的结论是______(填序号).
. 其中正确的结论是______(填序号).
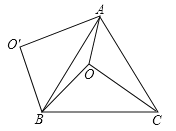
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)。

(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍画出图形。
(2)写出B、C两点的对应点B、C的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c的图象过点A(1,m),B(3,m),若点M(-2,y1),N(-1,y2),K(8,y3)也在二次函数y=x2+bx+c的图象上,将y1,y2,y3按从小到大的顺序用“<”连接,结果是___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
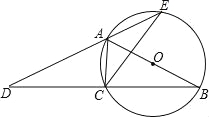
【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=BC.延长DA与⊙O的另一个交点为E,连接AC、CE.
(1)求证:∠B=∠D;
(2)若AB=13,BC﹣AC=7,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
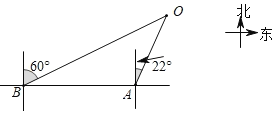
【题目】2019年4月23日是中国人民解放军海军成立70周年纪念日,届时将在青岛举行盛大的多国海军庆祝活动.为此我国海军进行了多次军事演习.如图,在某次军事演习时,舰艇A发现在他北偏东22°方向上有不明敌舰在指挥中心O附近徘徊,快速报告给指挥中心,此时在舰艇A正西方向50海里处的舰艇B接到返回指挥中心的行动指令,舰艇B迅速赶往在他北偏东60°方向的指挥中心处,舰艇B的速度是80海里/小时,请根据以上信息,求舰艇B到达指挥中心O的时间.(结果精确到0.1小时,参考数据:(sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,矩形ABCD的位置如图1所示,点A的坐标为(-2,0),点B的坐标为(0,2),点D的坐标为(-3,1).矩形ABCD以每秒1个单位长度的速度沿x轴正方向运动,设运动时间为x(0≤x≤3)秒,第一象限内的图形面积为y,则下列图象中表示y与x的函数关系的图象大致是
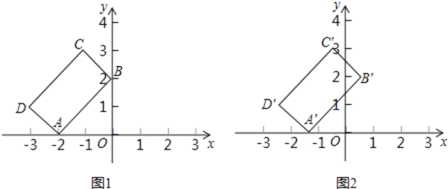
A. 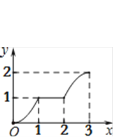 B.
B. 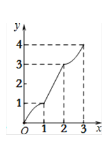 C.
C. 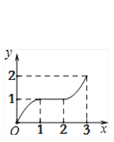 D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com