【题目】如图，在
中，点
在边
上，
，连接
交
于点
，则
的面积与四边形
的面积之比为（ ）
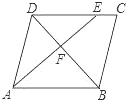
A. 3∶4 B. 9∶16 C. 9∶19 D. 9∶28
【答案】C
【解析】
由DE：EC=3：1，可得DF：FB=3：4，根据在高相等的情况下三角形面积比等于底边的比，可得S△EFD：S△BEF=3：4，S△BDE：S△BEC=3：1，可求△DEF的面积与四边形BCEF的面积的比值．
连接BE
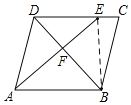
∵DE：EC=3：1
∴设DE=3k，EC=k，则CD=4k
∵ABCD是平行四边形
∴AB∥CD，AB=CD=4k
∴
∴S△EFD：S△BEF=3：4
∵DE：EC=3：1
∴S△BDE：S△BEC=3：1
设S△BDE=3a，S△BEC=a
则S△EFD=
，S△BEF=
∴SBCEF=S△BEC+S△BEF=
∴则△DEF的面积与四边形BCEF的面积之比9：19
故选C．
夺冠金卷全能练考系列答案科目：初中数学 来源： 题型：
【题目】某市政部门为了保护生态环境，计划购买A，B两种型号的环保设备．已知购买一套A型设备和三套B型设备共需230万元，购买三套A型设备和两套B型设备共需340万元．
（1）求A型设备和B型设备的单价各是多少万元；
（2）根据需要市政部门采购A型和B型设备共50套，预算资金不超过3000万元，问最多可购买A型设备多少套？
查看答案和解析>>
科目：初中数学 来源： 题型：
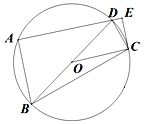
【题目】如图，四边形ABCD内接于⊙O，∠BAD=90°，过C作CE⊥AD垂足为E，且∠EDC=∠BDC.
（1）求证:CE是⊙O的切线；
（2）若DE+CE=4，AB=6，求BD的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】学生甲与乙学习概率初步知识后设计了如下游戏：甲手中有 
、
、
三张扑克牌，乙手中有 
、、
三张扑克牌，每局比赛时，两人从各自手中随机取一张牌进行比较，数字大的则本局获胜．
（1）若每人随机取出手中的一张牌进行比较，请列举出所有情况；
（2）求学生乙一局比赛获胜的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
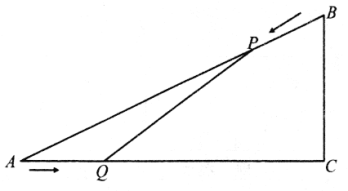
【题目】如图，已知
中，
cm，
cm，
cm．点
由
出发，以5cm/s的速度沿
向点
匀速运动，同时点
由出发，以4cm/s的速度沿
向点
匀速运动．连接
，设运动时间为
（单位：
，
）．
（1）求点到的距离（用含代数式表示）；
（2）求为何值时，线段将的面积分成的两部分的面积比为3∶13；
（3）当
为直角三角形时，求的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将矩形ABCD绕点A顺时针旋转α（0°＜α＜360°），得到矩形AEFG．
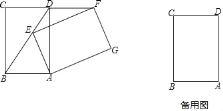
（1）如图，当点E在BD上时．求证：FD＝CD；
（2）当α为何值时，GC＝GB？画出图形，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某公园要建造一个圆形的喷水池，在水池中央垂直于水面竖一根柱子，上面的A处安装一个喷头向外喷水．连喷头在内，柱高0.8m．水流在各个方向上沿形状相同的抛物线路径落下，如图(1)所示．
根据设计图纸已知：如图(2)中所示直角坐标系中，水流喷出的高度y（m）与水平距离x（m）之间的函数关系式是 y＝﹣x2+2x+
．
(1)喷出的水流距水平面的最大高度是多少？
(2)如果不计其他因素，那么水池半径至少为多少时，才能使喷出的水流都落在水池内？
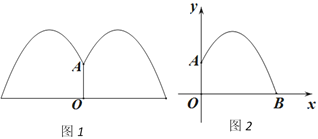
查看答案和解析>>
科目：初中数学 来源： 题型：
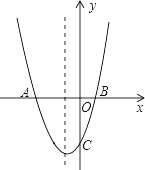
【题目】如图，已知：二次函数y=x2+bx+c 的图象与x轴交于A，B两点，其中A点坐标为（-3，0），与 y 轴交于点 C（0，-3）在抛物线上．
（1）求抛物线的表达式；
（2）抛物线的对称轴上有一动点 P，求出当 PB+PC 最小时点 P的坐标；
（3）若抛物线上有一动点Q，使△ABQ的面积为6，求Q点坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
