
【题目】AB为⊙O直径,BC为⊙O切线,切点为B,CO平行于弦AD,作直线DC.
(1)求证:DC为⊙O切线;
(2) 若AD·OC=8,求⊙O半径.
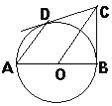
【答案】(1证明见解析;(2)2.
【解析】试题分析:①连接OD,要证明DC是 O的切线,只要证明∠ODC=90°即可.根据题意,可证△OCD≌△OCB,即可得∠CDO=∠CBO=90°,由此可证DC是 O的切线;
②连接BD,OD.先根据两角对应相等的两三角形相似证明△ADB∽△ODC,再根据相似三角形对应边成比例即可得到r的值.
试题解析:①证明:连接OD.
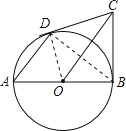
∵OA=OD,
∴∠A=∠ADO.
∵AD∥OC,
∴∠A=∠BOC,∠ADO=∠COD,
∴∠BOC=∠COD.
∵在△OBC与△ODC中,
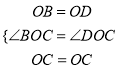 ,
,
∴△OBC≌△ODC(SAS),
∴∠OBC=∠ODC,
又∵BC是O的切线,
∴∠OBC=90°,
∴∠ODC=90°,
∴DC是O的切线;
②连接BD.
∵在△ADB与△ODC中,
![]()
∴△ADB∽△ODC,
∴AD:OD=AB:OC,
∴ADOC=ODAB=r2r=2r,即2r=8,
故r=2.


科目:初中数学 来源: 题型:
【题目】(1)如图1,∠AOB和∠COD都是直角
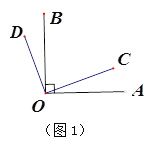
①若∠BOC=60°,则∠BOD= °,∠AOC= °;
②改变∠BOC的大小,则∠BOD与∠AOC相等吗?为什么?
(2)如图2,∠AOB=∠COD=80°,若∠AOD=∠BOC+40°,求∠AOC的度数;
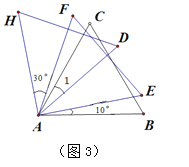
(3)如图3,将三个相同的等边三角形(三个内角都是60°)的一个顶点重合放置,若∠BAE=10°, ∠HAF=30°,则∠1= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两上数的和.现以这组数中的各个数作为正方形的边长构造如图1正方形:再分别依次从左到右取2个、3个、4个、5个正方形拼成如图2所示的长方形并记为①、②、③、④.若按此规律继续作长方形,则序号为⑧的长方形的周长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十一黄金周期间,泗县运河人家风景区门票价格为:成人票每张80元,学生票每张40元,泗县某中学七年级有x名学生和y名老师;八年级学生人数是七年级学生人数的![]() 倍,八年级老师人数是七年级老师人数的
倍,八年级老师人数是七年级老师人数的![]() 倍;若他们一起去风景区.
倍;若他们一起去风景区.
(1)两个年级在该景点的门票费用分别为:七年级 元;八年级 元;(用含x,y的代数式表示)
(2)若他们一起去风景区,则门票费用共需多少元?(用含x,y的代数式表示)若x=200,y=10,求两个年级门票费用的总和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com