
【题目】(1)如图1,∠AOB和∠COD都是直角
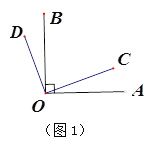
①若∠BOC=60°,则∠BOD= °,∠AOC= °;
②改变∠BOC的大小,则∠BOD与∠AOC相等吗?为什么?
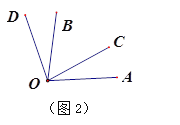
(2)如图2,∠AOB=∠COD=80°,若∠AOD=∠BOC+40°,求∠AOC的度数;
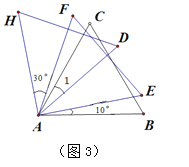
(3)如图3,将三个相同的等边三角形(三个内角都是60°)的一个顶点重合放置,若∠BAE=10°, ∠HAF=30°,则∠1= °.
【答案】(1) ① 30°, 30°, ②相等,同角的余角相等;(2)20°;(3)20°.
【解析】试题分析:(1)根据余角的性质即可得到结论; (2)根据角的和差即可得到结果; (3)根据等边三角形的性质得到∠DAH=∠EAF=∠BAC=60°,根据角的和差即可得到结论.
试题解析:
(1) ①∵∠AOB和∠COD都是直角,∠BOC=60°,
∴∠BOD=30°,∠AOC=30°;
②∠BOD=∠AOC,根据同角的余角相等可得结论;
(2) ∵∠AOB=∠COD=80°,
∴∠AOC=∠BOD=![]() ,
,
∵∠AOD=∠BOC+40°,
∴∠AOC=20°;
(3) ∵∠DAH=∠EAF=∠BAC=60°,
∴∠DAE=∠HAF=30°,
∴∠1=60°-30°-10°=20°.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
【题目】已知k>0,则函数y=-kx+k的图象经过第________象限( )
A. 一、二、三 B. 二、三、四 C. 一、二、四 D. 一、三、四
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2s,方差如下表:
选手 | 甲 | 乙 | 丙 | 丁 |
方差(s2) | 0.020 | 0.019 | 0.021 | 0.022 |
则这四人中发挥最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县2014年的GDP是250亿元,要使2016年的GDP达到360亿元,求这两年该县GDP年平均增长率.设年平均增长率为x,可列方程_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y= ![]() (k≠0),下列说法不正确的是( )
(k≠0),下列说法不正确的是( )
A.它的图像分布在第一、三象限
B.点(k,k)在它的图像上
C.它的图像关于原点对称
D.在每个象限内y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图像. 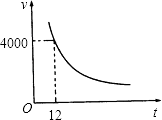
(1)请你根据图像提供的信息求出此蓄水池的蓄水量;
(2)求出此函数的解析式;
(3)若要6h排完水池中的水,那么每小时的排水量应该是多少?
(4)如果每小时排水量不超过5 000m3 , 那么水池中的水至少要多少小时排完?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2的图象向上平移1个单位,再向右平移2个单位所得图象的解析式是( )
A.y=(x+2)2+1B.y=(x﹣2)2+1C.y=(x﹣2)2﹣1D.y=(x+2)2﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家生产的一种新型节能灯,为了打开市场出台了相关政策:由厂家协调,厂家按成本价提供产品给经营户自主销售,成本价与出厂价之间的差价由厂家承担.李明按照相关政策投资销售本产品.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)李明在开始销售的第一个月将销售单价定为20元,那么厂家这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于3000元,那么厂家为他承担的总差价最少为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com