
【题目】将矩形ABCD绕点A顺时针旋转α(0°<α<360°),得到矩形AEFG.
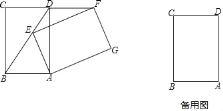
(1)如图,当点E在BD上时.求证:FD=CD;
(2)当α为何值时,GC=GB?画出图形,并说明理由.
【答案】(1)见解析;(2)见解析.
【解析】
(1)先运用SAS判定△AED≌△FDE,可得DF=AE,再根据AE=AB=CD,即可得出CD=DF;
(2)当GB=GC时,点G在BC的垂直平分线上,分两种情况讨论,依据∠DAG=60°,即可得到旋转角α的度数.
(1)由旋转可得,AE=AB,∠AEF=∠ABC=∠DAB=90°,EF=BC=AD,
∴∠AEB=∠ABE,
又∵∠ABE+∠EDA=90°=∠AEB+∠DEF,
∴∠EDA=∠DEF,
又∵DE=ED,
∴△AED≌△FDE(SAS),
∴DF=AE,
又∵AE=AB=CD,
∴CD=DF;
(2)如图,当GB=GC时,点G在BC的垂直平分线上,
分两种情况讨论:
①当点G在AD右侧时,取BC的中点H,连接GH交AD于M,
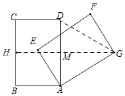
∵GC=GB,
∴GH⊥BC,
∴四边形ABHM是矩形,
∴AM=BH=![]() AD=
AD=![]() AG,
AG,
∴GM垂直平分AD,
∴GD=GA=DA,
∴△ADG是等边三角形,
∴∠DAG=60°,
∴旋转角α=60°;
②当点G在AD左侧时,同理可得△ADG是等边三角形,
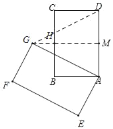
∴∠DAG=60°,
∴旋转角α=360°﹣60°=300°.


科目:初中数学 来源: 题型:
【题目】“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件获利减少2元.设每天安排x人生产乙产品.
(1)根据信息填表
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节期间,某食品店平均每天可卖出300只粽子,卖出1只粽子的利润是1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获取的利润更多,该店决定把零售单价下降m(0<m<1)元.
(1)零售单价下降m元后,该店平均每天可卖出_____只粽子,利润为_____元.
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元并且卖出的粽子更多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于函数![]() (k>0)有以下四个结论:
(k>0)有以下四个结论:
①这是y关于x的反比例函数;②当x>0时,y的值随着x的增大而减小;③函数图象与x轴有且只有一个交点;④函数图象关于点(0,3)成中心对称.
其中正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
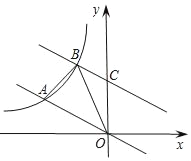
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() (k≠0)在第二象限内的图象相交于点A(m,1).
(k≠0)在第二象限内的图象相交于点A(m,1).
(1)求反比例函数的解析式;
(2)将直线y=﹣![]() x向上平移后与反比例函数图象在第二象限内交于点B,与y轴交于点C,且△ABO的面积为
x向上平移后与反比例函数图象在第二象限内交于点B,与y轴交于点C,且△ABO的面积为![]() ,求直线BC的解析式.
,求直线BC的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com