
【题目】若抛物线y=x2+bx(b>2)上存在关于直线y=x成轴对称的两个点,则b的取值范围是______.
【答案】b>3
【解析】
可设出对称的两个点P,Q的坐标,利用两点关于直线y=x成轴对称,可以设直线PQ的方程为y=-x+a,由于P、Q两点存在,所以方程组![]()
有两组不同的实数解,利用中点在直线上消去b,建立关于a的函数关系,求出变量a的范围.
解:设抛物线上关于直线l对称的两相异点为P(x1,y1)、Q(x2,y2),线段PQ的中点为M(x0,y0),设
直线PQ的方程为y=x+a,由于P、Q两点存在,
所以方程组![]() 有两组不同的实数解,
有两组不同的实数解,
即得方程x2+(1+b)x -a=0.①
判别式△=![]() -4
-4![]() >0.②
>0.②
由①得x0=![]() =-
=-![]() ,y0=-x0+a=
,y0=-x0+a=![]() +a
+a
∵M(x0,y0)在y=x上,x0=y0
∴-![]() +a ∴a=-b-1代入②解得b>3或b
+a ∴a=-b-1代入②解得b>3或b![]() -1
-1
∵b>2,∴b>3
故答案为:b>3


科目:初中数学 来源: 题型:
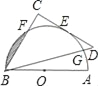
【题目】如图,AB为量角器(半圆O)的直径,等腰直角△BCD的斜边BD交量角器边缘于点G,直角边CD切量角器于读数为60°的点E处(即弧AE的度数为60°),第三边交量角器边缘于点F处.
(1)求量角器在点G处的读数α(90°<α<180°);
(2)若AB=12cm,求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,P是AB延长线上一点,PC与⊙O相切于点C,CD⊥AB于点D,过B点作AP的垂线交PC于点F.
(1)求证:E是CD的中点;
(2)若FB=FE=2,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市政部门为了保护生态环境,计划购买A,B两种型号的环保设备.已知购买一套A型设备和三套B型设备共需230万元,购买三套A型设备和两套B型设备共需340万元.
(1)求A型设备和B型设备的单价各是多少万元;
(2)根据需要市政部门采购A型和B型设备共50套,预算资金不超过3000万元,问最多可购买A型设备多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知A(2,0),B(1,-1),将线段OA绕点O逆时针旋转,旋转角为![]() (0°<
(0°<![]() <135°).记点A的对应点为A1,若点A1与点B的距离为
<135°).记点A的对应点为A1,若点A1与点B的距离为![]() ,则
,则![]() 为( ).
为( ).
A. 30° B. 45° C. 60° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红红和娜娜按如图所示的规则玩一次“锤子、剪刀、布”游戏,下列命题中错误的是( )

A.红红不是胜就是输,所以红红胜的概率为![]()
B.红红胜或娜娜胜的概率相等
C.两人出相同手势的概率为![]()
D.娜娜胜的概率和两人出相同手势的概率一样
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.
【1】从A、D、E、F四点中任意取一点,以所取的这一点及B、C为顶点三角形,则所画三角形是等腰三角形的概率是 ▲ ;
【2】从A、D、E、F四点中先后任意取两个不同的点,以所取的这两点及B、C为顶点画四边形,求所画四边形是平行四边形的概率(用树状图或列表求解).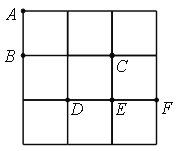
查看答案和解析>>
科目:初中数学 来源: 题型:
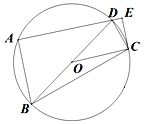
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,过C作CE⊥AD垂足为E,且∠EDC=∠BDC.
(1)求证:CE是⊙O的切线;
(2)若DE+CE=4,AB=6,求BD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形ABCD绕点A顺时针旋转α(0°<α<360°),得到矩形AEFG.
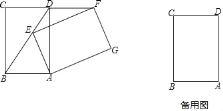
(1)如图,当点E在BD上时.求证:FD=CD;
(2)当α为何值时,GC=GB?画出图形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com