
【题目】如图,已知AB是⊙O的直径,P是AB延长线上一点,PC与⊙O相切于点C,CD⊥AB于点D,过B点作AP的垂线交PC于点F.
(1)求证:E是CD的中点;
(2)若FB=FE=2,求⊙O的半径.

【答案】(1)证明见解析;(2)2![]() .
.
【解析】
(1)延长BF、AC交于点M,则结合切线可得BF=FM,再结合平行线分线段成比例可求得CE=DE;
(2)结合条件可证得PF=AF,在Rt△PFB中,可得到PF和PB的关系,再结合PC是切线利用切割线定理可得到PB和PF的关系,可求得PB的长,则可求得AO的长,即⊙O的半径.
(1)证明:如图,延长BF、AC交于点M,
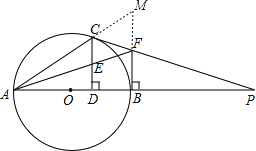
∵BF⊥AB,∴FB是⊙O的切线,
又CF是⊙O的切线,
∴CF=BF,
∴∠FCB=∠FBC,
又AB为直径,
∴∠BCM=90°,
∴∠CBM+∠M=∠BCF+∠FCM=90°,
∴∠FCM=∠M,
∴CF=MF,
∴BF=MF,
∵CD∥MB,
∴![]() ,
,
∴CE=ED,
即E是CD的中点;
(2)解:
∵BF=EF=2=FC=FM,
∴∠FCE=∠FEC=∠AED,
又CD⊥AB,
∴∠FAB+∠AED=∠ECF+∠P,
∴∠FAB=∠P,
∴AF=PF,
∴AB=PB,
设AB=PB=x,PF=y,
则在Rt△PBF中,由勾股定理可得y2=22+x2①,
又由切割线定理可得(y+2)2=x2x=2x2②,
则可解得x=4![]() ,y=6,
,y=6,
∴AO=![]() AB=2
AB=2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点E在AD边上,过点E作AB的平行线,交BC于点F,将矩形ABFE绕着点E逆时针旋转,使点F的对应点落在边CD上,点B的对应点N落在边BC上.
(1)求证:BF=NF;
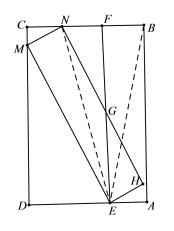
(2)已知AB=2,AE=1,求EG的长;
(3)已知∠MEF=30°,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近视镜镜片的焦距![]() (单位:米)是镜片的度数
(单位:米)是镜片的度数![]() (单位:度)的函数,下表记录了一组数据:
(单位:度)的函数,下表记录了一组数据:
| … | 100 | 250 | 400 | 500 | … |
| … | 1.00 | 0.40 | 0.25 | 0.20 | … |
(1)在下列函数中,符合上述表格中所给数据的是_________;
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(2)利用(1)中的结论计算:当镜片的度数为200度时,镜片的焦距约为________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如下表:
温度t/℃ | … | ﹣5 | ﹣3 | 2 | … |
植物高度增长量h/mm | … | 34 | 46 | 41 | … |
科学家推测出h(mm)与t之间的关系可以近似地用二次函数来刻画.已知温度越适合,植物高度增长量越大,由此可以推测最适合这种植物生长的温度为( )
A. ﹣2℃ B. ﹣1℃ C. 0℃ D. 1℃
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD 中,点 E,F 分别在 BC 和 AB 上,BE=3,AF=2,BF=4,将△ BEF 绕点 E 顺时针旋转,得到△GEH,当点 H 落在 CD 边上时,F,H 两点之间的距离为_____.
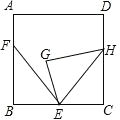
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com