
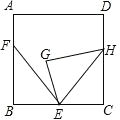
【题目】如图,正方形 ABCD 中,点 E,F 分别在 BC 和 AB 上,BE=3,AF=2,BF=4,将△ BEF 绕点 E 顺时针旋转,得到△GEH,当点 H 落在 CD 边上时,F,H 两点之间的距离为_____.
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是边AB、BC的中点,连接AF、DE相交于点G,连接CG.
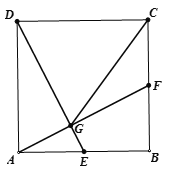
(1)求证:AF⊥DE;
(2)求证:CG=CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,若线段上的个点把这条线段分制为两部分,其中较长的一部分与全长之比等于![]() 时,则这个点称为黄金分割点。类比三角形中线的定义,我们规定:连接三角形的一个顶点和它对边的黄金分割点的线段叫做该三角形的黄金分割线.
时,则这个点称为黄金分割点。类比三角形中线的定义,我们规定:连接三角形的一个顶点和它对边的黄金分割点的线段叫做该三角形的黄金分割线.
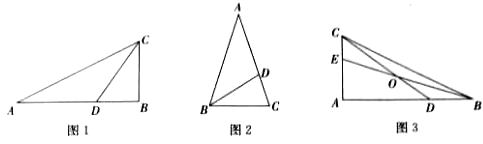
(1)如图1,CD是△ABC的黄金分割线(AD> BD),△ABC的面积为4,求△ACD的面积 ;
(2)如图2,在△ABC中,∠A= 36°,AB=AC=1,过点B作BD平分∠ABC,与AC相交于点D,求证: BD是△ABC的黄金分割线.
(3)如图3,BE、CD是△ABC的黄金分割线(AD> BD,AE> CE),BE、CD相交于点O.
①设△BOD与△COE的面积分别为S1、S2 ,请猜想S1、S2之间的数量关系,并说明理由;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,P是AB延长线上一点,PC与⊙O相切于点C,CD⊥AB于点D,过B点作AP的垂线交PC于点F.
(1)求证:E是CD的中点;
(2)若FB=FE=2,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
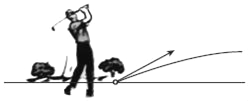
【题目】如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.
(1)求小球飞行3s时的高度;
(2)问:小球的飞行高度能否达到22m?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市政部门为了保护生态环境,计划购买A,B两种型号的环保设备.已知购买一套A型设备和三套B型设备共需230万元,购买三套A型设备和两套B型设备共需340万元.
(1)求A型设备和B型设备的单价各是多少万元;
(2)根据需要市政部门采购A型和B型设备共50套,预算资金不超过3000万元,问最多可购买A型设备多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知A(2,0),B(1,-1),将线段OA绕点O逆时针旋转,旋转角为![]() (0°<
(0°<![]() <135°).记点A的对应点为A1,若点A1与点B的距离为
<135°).记点A的对应点为A1,若点A1与点B的距离为![]() ,则
,则![]() 为( ).
为( ).
A. 30° B. 45° C. 60° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.
【1】从A、D、E、F四点中任意取一点,以所取的这一点及B、C为顶点三角形,则所画三角形是等腰三角形的概率是 ▲ ;
【2】从A、D、E、F四点中先后任意取两个不同的点,以所取的这两点及B、C为顶点画四边形,求所画四边形是平行四边形的概率(用树状图或列表求解).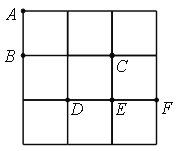
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com