练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

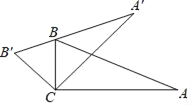
    【题目】如图，将△ABC绕顶点C逆时针旋转得到△A′B′C，且点B刚好落在A′B′上，若∠A＝25°，∠BCA′＝45°，求∠A′BA的度数．

    【答案】40°

    【解析】

    先利用旋转的性质得∠A′＝∠A＝25°，∠ABC＝∠B′，CB＝CB′，再利用等腰三角形的性质得∠B′＝∠CBB′，则根据三角形外角性质得∠CBB′＝70°，所以∠B′＝∠ABC＝70°，然后利用平角定义计算∠A′BA的度数．

    ∵△ABC绕顶点C逆时针旋转得到△A′B′C，且点B刚好落在A′B′上，

    ∴∠A′＝∠A＝25°，∠ABC＝∠B′，CB＝CB′，

    ∴∠B′＝∠CBB′，

    ∵∠CBB′＝∠A′+∠BCA′＝25°+45°＝70°，

    ∴∠B′＝70°，

    ∴∠ABC＝70°，

    ∴∠A′BA＝180°﹣70°﹣70°＝40°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】甲乙两人玩纸牌游戏，如图是同一副扑克中的 4 张扑克牌的正面，将它们正面朝下后放在桌上，甲先从中抽出一张，乙从剩余的 3 张牌中也抽出一张．

    （1）请用树状图表示出抽牌可能出现的所有结果．

    （2）甲说：“若抽出的两张牌上的数是一奇一偶，我获胜；否则，你获胜．”或按甲说的规则进行游戏，这个游戏公平吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，E、F分别是边AB、BC的中点，连接AF、DE相交于点G，连接CG．

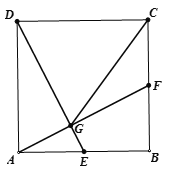
    （1）求证：AF⊥DE；

    （2）求证：CG=CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

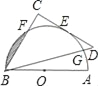
    【题目】如图，AB为量角器（半圆O）的直径，等腰直角△BCD的斜边BD交量角器边缘于点G，直角边CD切量角器于读数为60°的点E处（即弧AE的度数为60°），第三边交量角器边缘于点F处．

    （1）求量角器在点G处的读数α（90°＜α＜180°）；

    （2）若AB＝12cm，求阴影部分面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将正方形网格放置在平面直角坐标系中，其中每个小正方形的边长均为1，△ABC经过平移后得到△A1B1C1，若AC上一点P（1.2，1.4）平移后对应点为P1，点P1绕原点顺时针旋转180°，对应点为P2，则点P2的坐标为（　　）

    A. （2.8，3.6） B. （﹣2.8，﹣3.6）

    C. （3.8，2.6） D. （﹣3.8，﹣2.6）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

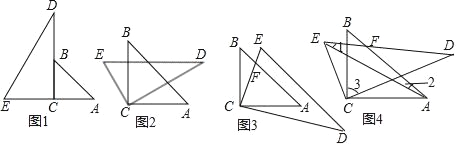
    【题目】将两块三角板按图1摆放，固定三角板ABC，将三角板CDE绕点C按顺时针方向旋转，其中∠A＝45°，∠D＝30°，设旋转角为α，（0°＜a＜80°）

    （1）当DE∥AC时（如图2），求α的值；

    （2）当DE∥AB时（如图3）．AB与CE相交于点F，求α的值；

    （3）当0°＜α＜90°时，连结AE（如图4），直线AB与DE相交于点F，试探究∠1+∠2+∠3的大小是否改变？若不改变，请求出此定值，若改变，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们知道，若线段上的个点把这条线段分制为两部分，其中较长的一部分与全长之比等于时，则这个点称为黄金分割点。类比三角形中线的定义，我们规定:连接三角形的一个顶点和它对边的黄金分割点的线段叫做该三角形的黄金分割线.

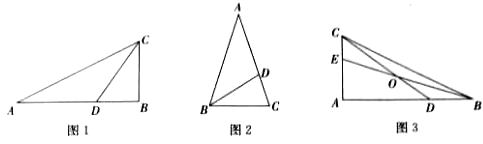
    (1)如图1，CD是△ABC的黄金分割线(AD> BD)，△ABC的面积为4,求△ACD的面积 ；

    (2)如图2,在△ABC中,∠A= 36°，AB=AC=1，过点B作BD平分∠ABC，与AC相交于点D，求证: BD是△ABC的黄金分割线.

    (3)如图3，BE、CD是△ABC的黄金分割线(AD> BD，AE> CE)，BE、CD相交于点O.

    ①设△BOD与△COE的面积分别为S1、S2 ,请猜想S1、S2之间的数量关系,并说明理由；

    ②求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AB是⊙O的直径，P是AB延长线上一点，PC与⊙O相切于点C，CD⊥AB于点D，过B点作AP的垂线交PC于点F．

    （1）求证：E是CD的中点；

    （2）若FB=FE=2，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在3×3的方格纸中，点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上.

    【1】从A、D、E、F四点中任意取一点，以所取的这一点及B、C为顶点三角形，则所画三角形是等腰三角形的概率是 ▲ ；

    【2】从A、D、E、F四点中先后任意取两个不同的点，以所取的这两点及B、C为顶点画四边形，求所画四边形是平行四边形的概率（用树状图或列表求解）.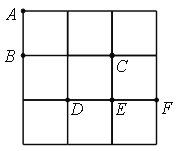

    查看答案和解析>>

    同步练习册答案