
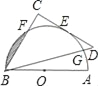
【题目】如图,AB为量角器(半圆O)的直径,等腰直角△BCD的斜边BD交量角器边缘于点G,直角边CD切量角器于读数为60°的点E处(即弧AE的度数为60°),第三边交量角器边缘于点F处.
(1)求量角器在点G处的读数α(90°<α<180°);
(2)若AB=12cm,求阴影部分面积.
【答案】(1)量角器在点G处的读数α=150°;(2)阴影部分的面积为(6π﹣9![]() )cm2.
)cm2.
【解析】
(1)连接OE,OF,则OE⊥CD,由BD为等腰直角△BCD的斜边,则BC⊥CD,从而求得∠D=∠CBD,进而得出∠ABG的度数,则可求得α为150°;
(2)根据已知可得出△OBF为正三角形,则∠BOF=60°,再求得S扇形和S△OBF,从而得出S阴影即可.
连接OE,OF,

(1)∵CD切半圆O于点E,
∴OE⊥CD,
∵BD为等腰直角△BCD的斜边,
∴BC⊥CD,∠D=∠CBD=45°,
∴OE∥BC,
∴∠ABC=∠AOE=60°,
∴∠ABG=∠ABC﹣∠CBD=60°﹣45°=15°,
∴弧AG的度数=2∠ABG=30°,
∴量角器在点G处的读数α=150°;
(2)∵OF=OB=![]() AB=6cm,∠ABC=60°,
AB=6cm,∠ABC=60°,
∴△OBF为正三角形,∠BOF=60°,
∴S扇形=![]() =6π(cm2),S△OBF=
=6π(cm2),S△OBF=![]() ×62=9
×62=9![]() (cm2),
(cm2),
∴S阴影=S扇形﹣S△OBF=(6π﹣9![]() )cm2
)cm2
∴阴影部分的面积为(6π﹣9![]() )cm2.
)cm2.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点E在AD边上,过点E作AB的平行线,交BC于点F,将矩形ABFE绕着点E逆时针旋转,使点F的对应点落在边CD上,点B的对应点N落在边BC上.
(1)求证:BF=NF;
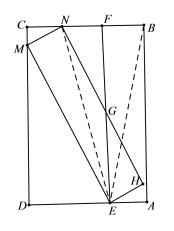
(2)已知AB=2,AE=1,求EG的长;
(3)已知∠MEF=30°,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达![]() 处时,测得小岛
处时,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛
方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向.如果航母继续航行至小岛
方向.如果航母继续航行至小岛![]() 的正南方向的
的正南方向的![]() 处,求还需航行的距离
处,求还需航行的距离![]() 的长.
的长.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1、x2是关于x的方程x2+2x+2k﹣4=0两个实数根,并且x1≠x2.
(1)求实数k的取值范围;
(2)若k为正整数,且该方程的根都是整数,求k的值;
(3)若|x1﹣x2|=6,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com