
����Ŀ�����������ǰ尴ͼ1�ڷţ��̶����ǰ�ABC�������ǰ�CDE�Ƶ�C��˳ʱ�뷽����ת�����С�A��45�㣬��D��30�㣬����ת��Ϊ������0�㣼a��80�㣩
��1����DE��ACʱ����ͼ2���������ֵ��
��2����DE��ABʱ����ͼ3����AB��CE�ཻ�ڵ�F�������ֵ��
��3����0�㣼����90��ʱ������AE����ͼ4����ֱ��AB��DE�ཻ�ڵ�F����̽����1+��2+��3�Ĵ�С�Ƿ�ı䣿�����ı䣬������˶�ֵ�����ı䣬��˵�����ɣ�
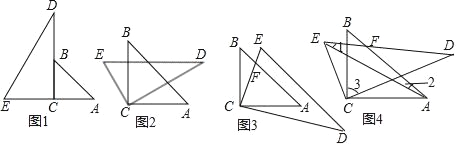
���𰸡���1��60�㣻
��2��105�㣻
��3�����䣬��ֵΪ105�㣮
��������
��1����DE��AC�ɵ���DCA����D��30�㣬�������������DCB��60�㣻
��2����DE��AB�ɵ���E����AFC��60�㣬�����������ڽǺͿ�����FCA��75�㼴������ACD��15�㣬�����������
��3�������������ڽǺͺ���ǵ��ڲ����ڵ������ڽǺͣ��г���1����2����3��ϵʽ������1+��2+��3��ֵ.
��1����DE��AC��
���D����ACD��30�㣬
���ߡ�BCA��90�㣬
���BCD����BCA����ACD��60�㣬������60�㣻
��2����DE��AB��
���E����CFA��60�㣬
���ߡ�CFA����B+��BCE��
���BCE��15�㣬
���BCD����ECD+��BCE��105�㣬������105�㣻
��3����С���䣬��ֵΪ105�㣬
�ߡ�ACD+��CAB����D+��AFD����CAB��45�㣬��D��30�㣬
���AFD����ACD��15�㣬
���ߡ�1+��2����AFD����3��90�㩁��ACD��
���1+��2+��3����AFD+90�㩁��ACD��90��+15�㣽105��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������A��B������Ʒ��ÿ�ι���ͬһ����Ʒ�ĵ�����ͬ��������Ϣ���±���
���� | ������������ | �����ܷ��ã�Ԫ | |
A | B | ||
��һ�� | 2 | 1 | 55 |
�ڶ��� | 1 | 3 | 65 |
����������Ϣ����������⣺
��1����A��B������Ʒ�ĵ��ۣ�
��2���������ι�����������Ʒ��12������A����Ʒ������������B����Ʒ������2��������Ƴ���ʡǮ�Ĺ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ҹ���ȫ������ơ�������������ҹ�����ĸ��2018��5�³ɹ���ɵ�һ�κ�����������.��ͼ����ĸ�������У�����![]() ��ʱ�����С��
��ʱ�����С��![]() λ�����ı�ƫ��
λ�����ı�ƫ��![]() �������뺽ĸ���80����ٺ���һ��ʱ���B�������С��
�������뺽ĸ���80����ٺ���һ��ʱ���B�������С��![]() λ�����ı�ƫ��
λ�����ı�ƫ��![]() ����.�����ĸ����������С��
����.�����ĸ����������С��![]() �����Ϸ����
�����Ϸ����![]() �������躽�еľ���
�������躽�еľ���![]() �ij�.
�ij�.
���ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
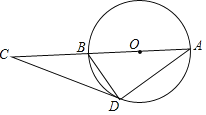
����Ŀ����ͼ��CD�ǡ�O�����ߣ���C��ֱ��AB���ӳ����ϣ�
��1����֤����CAD=��BDC��
��2����BD=![]() AD��AC=3����CD�ij���
AD��AC=3����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
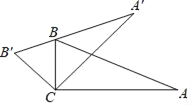
����Ŀ����ͼ������ABC�ƶ���C��ʱ����ת�õ���A��B��C���ҵ�B�պ�����A��B���ϣ�����A��25�㣬��BCA�䣽45�㣬���A��BA�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
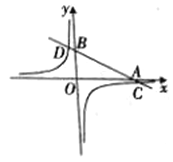
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y= kx +b(k��0)��ͼ��ֱ�x�ᡢy����A��B���㣬�뷴��������y=![]() (m��0)��ͼ����C��D���㡣��֪��C��������(6��-1)��D(n��3).
(m��0)��ͼ����C��D���㡣��֪��C��������(6��-1)��D(n��3).
(1)��m��ֵ�͵�D�����ꣻ
(2)���߶�AB�ij��ȣ�
(3)����ͼ��ֱ��д��: ��xΪ��ֵʱ��һ�κ�����ֵ���ڷ�����������ֵ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ϵ����������![]() ��ͼ������ͼ�����������⣺
��ͼ������ͼ�����������⣺
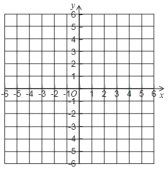
��1����![]() �Ľ⣺
�Ľ⣺
��2����ʽ![]() �Ľ⼯��
�Ľ⼯��
��3����![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ��Ϊ���Ʋ����ʺ�ij������ֲ���������¶ȣ�������ֲ��ֱ���ڲ�ͬ�¶ȵĻ����У�����һ��ʱ����Գ�����ֲ��߶ȵ���������������������±���
�¶�t/�� | �� | ��5 | ��3 | 2 | �� |
ֲ��߶�������h/mm | �� | 34 | 46 | 41 | �� |
��ѧ���Ʋ��h��mm����t֮��Ĺ�ϵ���Խ��Ƶ��ö��κ������̻�����֪�¶�Խ�ʺϣ�ֲ��߶�������Խ���ɴ˿����Ʋ����ʺ�����ֲ���������¶�Ϊ��������
A. ��2�� B. ��1�� C. 0�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Բ���棨�����м���һ��ֱ��Ϊ1m��Բ�������Ϸ��ĵ��ݣ�����һ���㣩�����Ĺ�������ƽ���ڵ����������ڵ������γ���ͼ��ʾ��Բ������Ӱ����֪����ֱ��Ϊ2m�����������1m�������������2m�������Բ������Ӱ������ǣ�������
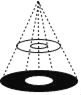
A. 2��m2 B. 3��m2 C. 6��m2 D. 12��m2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com