
【题目】红红和娜娜按如图所示的规则玩一次“锤子、剪刀、布”游戏,下列命题中错误的是( )

A.红红不是胜就是输,所以红红胜的概率为![]()
B.红红胜或娜娜胜的概率相等
C.两人出相同手势的概率为![]()
D.娜娜胜的概率和两人出相同手势的概率一样
科目:初中数学 来源: 题型:
【题目】科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如下表:
温度t/℃ | … | ﹣5 | ﹣3 | 2 | … |
植物高度增长量h/mm | … | 34 | 46 | 41 | … |
科学家推测出h(mm)与t之间的关系可以近似地用二次函数来刻画.已知温度越适合,植物高度增长量越大,由此可以推测最适合这种植物生长的温度为( )
A. ﹣2℃ B. ﹣1℃ C. 0℃ D. 1℃
查看答案和解析>>
科目:初中数学 来源: 题型:
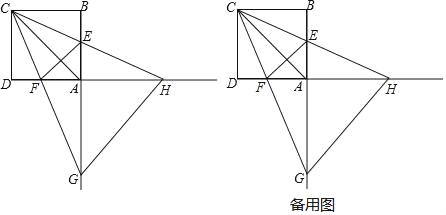
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.
查看答案和解析>>
科目:初中数学 来源: 题型:
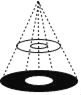
【题目】圆桌面(桌面中间有一个直径为1m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为2m,桌面离地面1m,若灯泡离地面2m,则地面圆环形阴影的面积是( )
A. 2πm2 B. 3πm2 C. 6πm2 D. 12πm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线 y=ax2﹣5ax+c 交 x 轴于点 A,点 A 的坐标为(4,0).
(1)用含 a 的代数式表示 c.
(2)当 a=![]() 时,求 x 为何值时 y 取得最小值,并求出 y 的最小值.
时,求 x 为何值时 y 取得最小值,并求出 y 的最小值.
(3)当 a=![]() 时,求 0≤x≤6 时 y 的取值范围.
时,求 0≤x≤6 时 y 的取值范围.
(4)已知点 B 的坐标为(0,3),当抛物线的顶点落在△AOB 外接圆内部时,直接写出 a的取值范围.
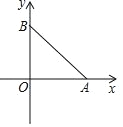
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件获利减少2元.设每天安排x人生产乙产品.
(1)根据信息填表
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com