
【题目】如图,在平面直角坐标系中,抛物线 y=ax2﹣5ax+c 交 x 轴于点 A,点 A 的坐标为(4,0).
(1)用含 a 的代数式表示 c.
(2)当 a=![]() 时,求 x 为何值时 y 取得最小值,并求出 y 的最小值.
时,求 x 为何值时 y 取得最小值,并求出 y 的最小值.
(3)当 a=![]() 时,求 0≤x≤6 时 y 的取值范围.
时,求 0≤x≤6 时 y 的取值范围.
(4)已知点 B 的坐标为(0,3),当抛物线的顶点落在△AOB 外接圆内部时,直接写出 a的取值范围.
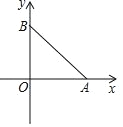
【答案】(1)c=4a;(2)当 x=![]() 时,y 取得最小值,最小值为﹣
时,y 取得最小值,最小值为﹣![]() ;(3)当 0≤x≤6 时,y 的取值范围是﹣5≤y≤
;(3)当 0≤x≤6 时,y 的取值范围是﹣5≤y≤![]() ;(4)-
;(4)-![]() ﹣
﹣![]() <a<﹣
<a<﹣![]() +
+![]() 且 a≠0.
且 a≠0.
【解析】
(1)由抛物线和x轴的交点A的坐标代入即可求出
(2)已知a的值可求出c的值,从而可以求出抛物线的解析式;再把抛物线的解析式用配方法表示出来,根据抛物线的性质特点求出
(3)已知a的值求出b,从而求出抛物线的解析式;把抛物线用配方法表示出来根据其性质可求出y的取值范围
(4)把抛物线的解析式用配方法表示出来求出其对称轴和定点坐标,根据题意作出圆在进行分析解答
(1)将 A(4,0)代入 y=ax2﹣5ax+c,得:16a﹣20a+c=0,解得:c=4a.
(2)当 a=![]() 时,c=2,
时,c=2,
∴抛物线的解析式为 y=![]() x2﹣
x2﹣ ![]() x+2=
x+2=![]() (x﹣
(x﹣![]() )2﹣
)2﹣ ![]() .
.
∵a= ![]() >0,
>0,
∴当 x=![]() 时,y 取得最小值,最小值为﹣
时,y 取得最小值,最小值为﹣![]() .
.
(3)当 a=﹣![]() 时,c=﹣2,
时,c=﹣2,
∴抛物线的解析式为 y=﹣![]() x2+
x2+ ![]() x﹣2=﹣
x﹣2=﹣![]() (x﹣
(x﹣ ![]() )2+
)2+ ![]() .
.
∵a=﹣![]() <0,
<0,
∴当 x=![]() 时,y 取得最大值,最大值为
时,y 取得最大值,最大值为![]() ; 当 x=0 时,y=﹣2;
; 当 x=0 时,y=﹣2;
当 x=6 时,y=﹣![]() ×62+
×62+ ![]() ×6﹣2=﹣5.
×6﹣2=﹣5.
∴当 0≤x≤6 时,y 的取值范围是﹣5≤y≤![]() .
.
(4)∵抛物线的解析式为 y=ax2﹣5ax+4a=a(x﹣![]() )2﹣
)2﹣ ![]() a,
a,
∴抛物线的对称轴为直线 x=![]() ,顶点坐标为(
,顶点坐标为(![]() ,﹣
,﹣![]() a).
a).
设线段 AB 的中点为 O,以 AB 为直径作圆,设抛物线对称轴与⊙O 交于点 C,D,过点 O
作 OH⊥CD 于点 H,如图所示.
∵点 A 的坐标为(4,0),点 B 的坐标(0,3),
∴AB=5,点 O 的坐标为(2,![]() ),点 H 的坐标为(
),点 H 的坐标为(![]() ,
,![]() ).在 Rt△COH 中,
).在 Rt△COH 中,
OC=![]() AB=
AB= ![]() ,OH=
,OH= ![]() ,
,
∴CH= ![]() ,
,
∴点 C 的坐标为(![]() ,
,![]() ).
).
同理:点 D 的坐标为(![]() ,﹣
,﹣![]() ),
),
∴ ![]()
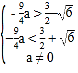
![]() ,
,
解得:﹣![]() -
-![]() <a<﹣
<a<﹣![]() +
+![]() 且 a≠0.
且 a≠0.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
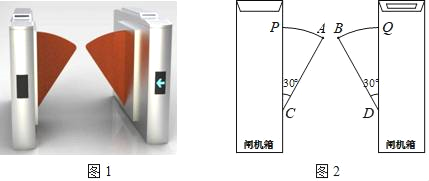
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红红和娜娜按如图所示的规则玩一次“锤子、剪刀、布”游戏,下列命题中错误的是( )

A.红红不是胜就是输,所以红红胜的概率为![]()
B.红红胜或娜娜胜的概率相等
C.两人出相同手势的概率为![]()
D.娜娜胜的概率和两人出相同手势的概率一样
查看答案和解析>>
科目:初中数学 来源: 题型:
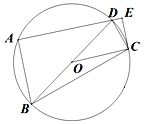
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,过C作CE⊥AD垂足为E,且∠EDC=∠BDC.
(1)求证:CE是⊙O的切线;
(2)若DE+CE=4,AB=6,求BD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
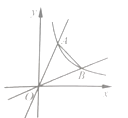
【题目】如图,在平面直角坐标系中,反比例函数![]() (x>0)与正比例函数y=kx、
(x>0)与正比例函数y=kx、 ![]() (k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
(k>1)的图象分别交于点A、B,若∠AOB=45°,则△AOB的面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生甲与乙学习概率初步知识后设计了如下游戏:甲手中有 ![]() 、
、![]() 、
、![]() 三张扑克牌,乙手中有
三张扑克牌,乙手中有 ![]() 、
、![]() 、
、![]() 三张扑克牌,每局比赛时,两人从各自手中随机取一张牌进行比较,数字大的则本局获胜.
三张扑克牌,每局比赛时,两人从各自手中随机取一张牌进行比较,数字大的则本局获胜.
(1)若每人随机取出手中的一张牌进行比较,请列举出所有情况;
(2)求学生乙一局比赛获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
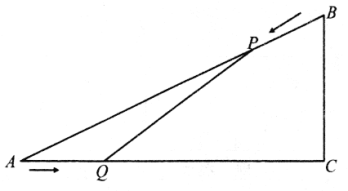
【题目】如图,已知![]() 中,
中,![]() cm,
cm,![]() cm,
cm,![]() cm.点
cm.点![]() 由
由![]() 出发,以5cm/s的速度沿
出发,以5cm/s的速度沿![]() 向点
向点![]() 匀速运动,同时点
匀速运动,同时点![]() 由
由![]() 出发,以4cm/s的速度沿
出发,以4cm/s的速度沿![]() 向点
向点![]() 匀速运动.连接
匀速运动.连接![]() ,设运动时间为
,设运动时间为![]() (单位:
(单位:![]() ,
,![]() ).
).
(1)求点![]() 到
到![]() 的距离(用含
的距离(用含![]() 代数式表示);
代数式表示);
(2)求![]() 为何值时,线段
为何值时,线段![]() 将
将![]() 的面积分成的两部分的面积比为3∶13;
的面积分成的两部分的面积比为3∶13;
(3)当![]() 为直角三角形时,求
为直角三角形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
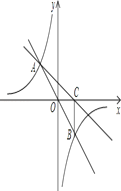
【题目】如图,在直角坐标系xOy中,直线y=mx与双曲线![]() 相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
(1)求m、n的值;
(2)求直线AC的解析式.
(3)点P在双曲线上,且△POC的面积等于△ABC面积的![]() ,求点P的坐标。
,求点P的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com