
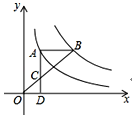
【题目】如图,在直角坐标系xOy中,直线y=mx与双曲线![]() 相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
相交于A(﹣1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
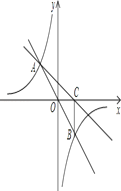
(1)求m、n的值;
(2)求直线AC的解析式.
(3)点P在双曲线上,且△POC的面积等于△ABC面积的![]() ,求点P的坐标。
,求点P的坐标。
【答案】(1)m=-2,n=-2(2)y=-x+1(3)(2,-1)或(-2,1)
【解析】
(1)由题意,根据对称性得到B的横坐标为1,确定出C的坐标,根据三角形AOC的面积求出A的纵坐标,确定出A坐标,将A坐标代入一次函数与反比例函数解析式,即可求出m与n的值;
(2)设直线AC解析式为y=kx+b,将A与C坐标代入求出k与b的值,即可确定出直线AC的解析式.
(3)根据双曲线的对称性求得B(1,-2),求出三角形ABC的面积,设点P(a,![]() ),再根据S△POC=
),再根据S△POC=![]() S△ABC,列出关于a的方程即可。
S△ABC,列出关于a的方程即可。
(1)∵直线y=mx与双曲线y=![]() 相交于A(-1,a)、B两点,
相交于A(-1,a)、B两点,
∴B点横坐标为1,∵BC⊥x轴,则C(1,0),
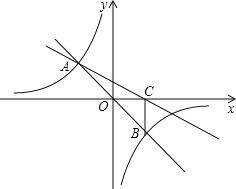
∵△AOC的面积为1,
∴A(-1,2),
将A(-1,2)代入y=mx,y=![]() 可得m=-2,n=-2;
可得m=-2,n=-2;
(2)设直线AC的解析式为y=kx+b,
∵y=kx+b经过点A(-1,2)、C(1,0)
∴![]() ,
,
解得k=-1,b=1,
∴直线AC的解析式为y=-x+1;
(3)由对称性可得B(1,-2),
∴S△ABC=![]() =2,
=2,
设点P(a,![]() ),
),
∵S△POC=![]() S△ABC,
S△ABC,
∴S△POC=![]() ,
,
解得a=2或-2,
∴点P的坐标为(2,-1)或(-2,1).


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线 y=ax2﹣5ax+c 交 x 轴于点 A,点 A 的坐标为(4,0).
(1)用含 a 的代数式表示 c.
(2)当 a=![]() 时,求 x 为何值时 y 取得最小值,并求出 y 的最小值.
时,求 x 为何值时 y 取得最小值,并求出 y 的最小值.
(3)当 a=![]() 时,求 0≤x≤6 时 y 的取值范围.
时,求 0≤x≤6 时 y 的取值范围.
(4)已知点 B 的坐标为(0,3),当抛物线的顶点落在△AOB 外接圆内部时,直接写出 a的取值范围.
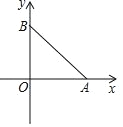
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件获利减少2元.设每天安排x人生产乙产品.
(1)根据信息填表
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的书包里只放了A4大小的试卷共4张,其中语文2张、数学1张、英语1张.
![]() 若随机地从书包中抽出2张,求抽出的试卷中有英语试卷的概率为______;
若随机地从书包中抽出2张,求抽出的试卷中有英语试卷的概率为______;
![]() 若随机地从书包中抽出3张,抽出的试卷中有英语试卷的概率为______.
若随机地从书包中抽出3张,抽出的试卷中有英语试卷的概率为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于函数![]() (k>0)有以下四个结论:
(k>0)有以下四个结论:
①这是y关于x的反比例函数;②当x>0时,y的值随着x的增大而减小;③函数图象与x轴有且只有一个交点;④函数图象关于点(0,3)成中心对称.
其中正确的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
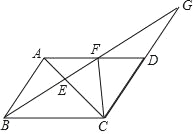
【题目】如图,AC是ABCD的对角线,在AD边上取一点F,连接BF交AC于点E,并延长BF交CD的延长线于点G.
(1)若∠ABF=∠ACF,求证:CE2=EFEG;
(2)若DG=DC,BE=6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)求证:无论m为任何实数,此函数图象与x轴总有两个交点;
(2)若此函数图象与x轴的一个交点为(-3,0),求此函数图象与x轴的另一个交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=![]() DQ,求点F的坐标.
DQ,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y=![]() 上,点B在双曲线y=
上,点B在双曲线y=![]() (k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k=__.
(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k=__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com