
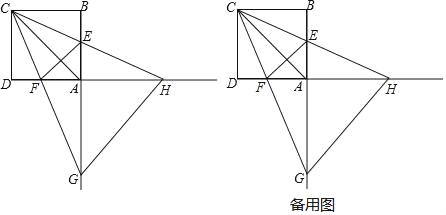
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4����E��F�ֱ��ڱ�AB��AD�ϣ��ҡ�ECF��45�㣬CF���ӳ��߽�BA���ӳ����ڵ�G��CE���ӳ��߽�DA���ӳ����ڵ�H������AC��EF����GH��
��1����գ���AHC�� ����ACG�������������������
��2���߶�AC��AG��AHʲô��ϵ����˵�����ɣ�
��3����AE��m��
�١�AGH�����S�б仯������仯�������S��m�ĺ�����ϵʽ��������仯���������ֵ��
����ֱ��д��ʹ��CGH�ǵ��������ε�mֵ��
���𰸡���1��=����2�����ۣ�AC2��AGAH�����ɼ���������3���١�AGH��������䣮��m��ֵΪ![]() ��3��12��6
��3��12��6![]() ��.
��.
��������
��1��֤����DAC=��AHC+��ACH=45�㣬��ACH+��ACG=45���������Ƴ���AHC=��ACG��
��2�����ۣ�AC2=AGAH��ֻҪ֤����AHC�ס�ACG���ɽ�����⣻
��3���١�AGH��������䣮���������ε������ʽ���㼴�ɣ�
�ڷ��������ηֱ���⼴�ɽ������.
��1�����ı���ABCD�������Σ�
��AB��CB��CD��DA��4����D����DAB��90����DAC����BAC��45�㣬
��AC��![]() ��
��
�ߡ�DAC����AHC+��ACH��45�㣬��ACH+��ACG��45�㣬
���AHC����ACG��
�ʴ�Ϊ����
��2�����ۣ�AC2��AGAH��
���ɣ��ߡ�AHC����ACG����CAH����CAG��135�㣬
���AHC�ס�ACG��
��![]() ��
��
��AC2��AGAH��
��3���١�AGH��������䣮
���ɣ���S��AGH��![]() AHAG��
AHAG��![]() AC2��
AC2��![]() ����4
����4![]() ��2��16��
��2��16��
���AGH�����Ϊ16��
����ͼ1�У���GC��GHʱ����֤��AHG�ա�BGC��
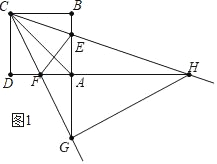
�ɵ�AG��BC��4��AH��BG��8��
��BC��AH��
��![]() ,
,
��AE��![]() AB��
AB��![]() ��
��
��ͼ2�У���CH��HGʱ��
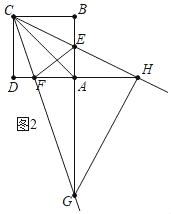
��֤AH��BC��4��
��BC��AH��
��![]() ��1��
��1��
��AE��BE��3��
��ͼ3�У���CG��CHʱ����֤��ECB����DCF��22.5��
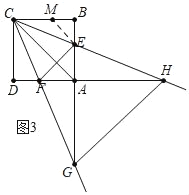
��BC��ȡһ��M��ʹ��BM��BE��
���BME����BEM��45�㣬
�ߡ�BME����MCE+��MEC��
���MCE����MEC��22.5�㣬
��CM��EM����BM��BE��m����CM��EM![]() m��
m��
��m+![]() m��6��
m��6��
��m��6��![]() ��1����
��1����
��AE��6��6��![]() ��1����12��6
��1����12��6![]() ��
��
��������������������m��ֵΪ![]() ��3��12��6
��3��12��6![]() ��
��


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=6��BC=4�����Խ���BD�е�O��ֱ�߷ֱ�AB��CD���ڵ�E��F��
��1����֤���ı���BEDF��ƽ���ı��Σ�
��2�����ı���BEDF������ʱ����EF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�OA��4��OC��8���ı���ABCO��ƽ���ı��Σ�
��1�����B�����꼰�ı���ABCO�������
��2������P�ӵ�C��2��λ����/����ٶ���CO�����ƶ���ͬʱ��Q�ӵ�O��1��λ����/����ٶ���OA�����ƶ������ƶ���ʱ��Ϊt�룬��AQB����BPC������ֱ��Ϊ![]() ��
��![]() ���ı���QBPO������Ƿ����仯�������䣬�����֤����Ľ��ۣ����仯������仯�ķ�Χ��
���ı���QBPO������Ƿ����仯�������䣬�����֤����Ľ��ۣ����仯������仯�ķ�Χ��
��3���ڣ�2���������£��Ƿ����ij��ʱͬ��ʹ![]() �������ڣ����t��ֵ���������ڣ���˵�����ɣ�
�������ڣ����t��ֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������IJ��ڴ���װ�аס��졢��������ɫ��С�����dz�����ɫ֮��û�������������а���2ֻ������1ֻ������1ֻ. ���е����Ѿ����ȣ�
��1������شӴ�������1ֻ������������ĸ����Ƕ��٣�
��2������شӴ�������1ֻ�Żؽ����������ڶ�����.�����û���״ͼ���б��ķ�����ʾ���еȿ��ܵĽ�����������ζ���������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
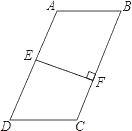
����Ŀ����ͼ�����ı���ABCD�У�AB��DC��E��AD�е㣬EF��BC�ڵ�F��BC=5��EF=3��
��1����AB=DC�����ı���ABCD�����S=__��
��2����AB��DC�����ʱ�ı���ABCD�����S��__S���á�������=��������գ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�E��F��G��H�ֱ��DZ�AB��BC��CD��DA���е㣮���ı���EFGHΪ���Σ���Խ���AC��BDӦ��������__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽���⣺

��1����ͼ1����AB��CD�����B+��D����E������˵��������
��2����֮������B+��D����E��ֱ��AB��ֱ��CD��ʲôλ�ù�ϵ����Ҫ˵�����ɣ�
��3��������E����ͼ2��λ�ã���ʱ��B����D����E֮����ʲô��ϵ��ֱ��д�����ۣ�
��4��������E����ͼ3��λ�ã���ʱ��B����D����E֮����ʲô��ϵ��ֱ��д�����ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ʶ���ɣ������Ѿ�֪����ͨ�����㼸��ͼ�ε�������Ա�ʾһЩ�������ʽ������ͼ1���Եõ���a+b��2��a2+2ab+b2�����ڴˣ������������⣺

��1������ͼ2��д��һ���������ʽ���� ����
��2�����ã�1���еõ��Ľ��ۣ������������⣺��a+b+c��10��ab+ac+bc��35����a2+b2+c2���� ����
��3��С��ͬѧ��ͼ3��x�ű߳�Ϊa�������Σ�y�ű߳�Ϊb�������Σ�z�ſ������ֱ�Ϊa��b�ij�����ֽƬƴ��һ�����Ϊ��2a+b����a+2b�������Σ���x+y+z���� ����
��֪ʶǨ�ƣ���4����ʵ�ϣ�ͨ�����㼸��ͼ�ε����Ҳ���Ա�ʾһЩ�������ʽ��ͼ4��ʾ����һ���߳�Ϊx����������ȥһ��С�����������ƴ��һ���³����壬�������ͼ4��ͼ�εı仯��ϵ��д��һ���������ʽ���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
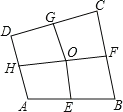
����Ŀ����ͼ���ı���ABCD�У�E��F��G��H�����Ǹ����е㣬O������һ�㣬���ı���AEOH���ı���BFOE���ı���CGOF������ֱ�Ϊ6��7��8���ı���DHOG���Ϊ______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com